题目内容
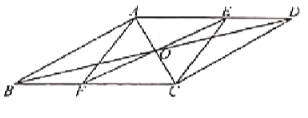
【题目】如图,四边形ABCD是平行四边形,点E、F在BC上,且CF=BE,连接DE,过点F作FG⊥AB于点G.

(1)如图1,若∠B=60°,DE平分∠ADC,且 ![]() ,
,![]() ,求平行四边形ABCD的面积.
,求平行四边形ABCD的面积.
(2)点H在GF上,且HE=HF,延长EH交AC,CD于点O,Q,连接AQ,若AC=BC=EQ,∠EQC=45°,求证:![]() .
.
【答案】(1)18![]() +9;(2)见详解.
+9;(2)见详解.
【解析】
(1)由角平分线的定义及平行四边形的性质,得CD=CE=6,从而得CF=![]() ,进而得BC=6+
,进而得BC=6+![]() .过点A作AM⊥BC于点M,得AM=
.过点A作AM⊥BC于点M,得AM= ![]() ,根据平行四边形的面积公式,即可求解.
,根据平行四边形的面积公式,即可求解.
(2)过点C作CN⊥EQ于点N,其延长线交AD于点K,先证△BGF≌△CNE(AAS),再证△ACK≌△QEC(ASA),进而即可得到结论.
(1)∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠CED,
∴∠CED=∠CDE,
∴CD=CE=6,
∵![]() ,
,
∴CF=![]() ,
,
∵CF=BE,
∴BE=![]() ,
,
∴BC=6+![]() .
.
过点A作AM⊥BC于点M,
∵∠B=60°,AB=CD=6,
∴∠BAM=30°,
∴BM=3,
∴AM=![]() BM=
BM=![]() ,
,
∴平行四边形ABCD的面积=(6+![]() )×
)×![]() =18
=18![]() +9;
+9;
(2)过点C作CN⊥EQ于点N,其延长线交AD于点K,
∵∠EQC=45°,
∴△CNQ为等腰直角三角形,
∴∠NQC=∠NCQ=45°,且CQ=![]() CN,
CN,
∵HE=HF,
∴∠HEF=∠HFE,
∵FG⊥AB,CN⊥EQ,
∴∠FGB=∠ENC=90°,
又∵BE=CF,
∴BF=CE,
∴△BGF≌△CNE(AAS),
∴BG=CN,∠B=∠ECN,
∴CQ=![]() BG,
BG,
又∵AC=BC=AD,
∴∠D=∠ACD,
又∵∠B=∠D,
∴∠ECN=∠ACD,
∴∠KAC=∠BCA=∠NCQ=45°,
∴∠BAC=∠ACD=∠B=∠CDA=∠ECN =67.5°,
∴∠ACK= ∠ECN-∠BCA =22.5°,∠QEC=180°-90°-∠ECN =22.5°,
即:∠ACK=∠QEC,
又∵∠KAC=∠CQE=45°,AC=QE,
∴△ACK≌△QEC(ASA),
∴CK=CE,
∵∠CDA=67.5°,∠NCQ=45°,
∴∠CKD=180°-45°-67.5°=67.5°,
∴∠CKD=∠CDA,
∴CK=CD,
∴CE=CD,
∵CD=CQ+QD=![]() BG+DQ,
BG+DQ,
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案