Question

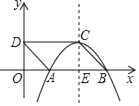
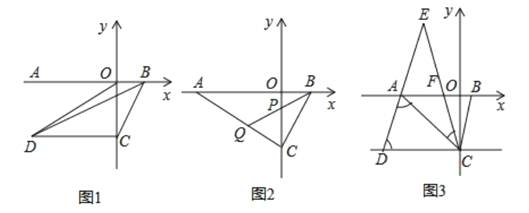
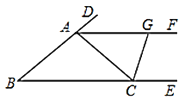
【题目】如图，△ACE是以平行四边行ABCD的对角线AC为边的等边三角形，点C与点E关于x轴对称．若E点的坐标是（10，-4 ），则D点的坐标是（ ）

A.（6，0）B.（6，0）C.（8，0）D.（8，0）

Answer 1

【答案】C

【解析】

设CE交x轴于点M，由△ACE是等边三角形，点C与点E关于x轴对称，E点的坐标是(10，-4 )，得AM=12，从而得AO=2，易证BOACMD，得DM=AO=2，进而即可求解．

设CE交x轴于点M，

∵△ACE是等边三角形，点C与点E关于x轴对称，E点的坐标是(10，-4 )，

∴CM⊥x轴，CM=EM=4，∠CAM=30°，OM=10，

∴AM=4×=12，

∴AO=12-10=2，

∵在平行四边行ABCD中，AB=CD，AB∥CD，

∴∠BAO=∠CDM，

又∵∠BOA=∠CMD=90°，

∴BOACMD（AAS），

∴DM=AO=2，

∴OD=OM-DM=10-2=8，

∴D(8，0)，

故选C．