题目内容
【题目】综合与探究
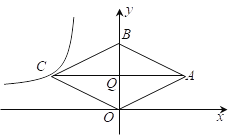
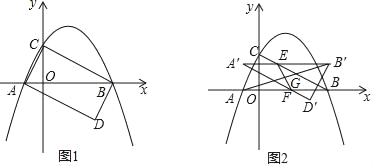
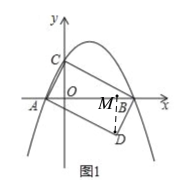
如图1,抛物线y=ax2+bx+2与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C,连接AC,BC.D为坐标平面第四象限内一点,且使得△ABD与△ABC全等.
(1)求抛物线的表达式.
(2)请直接写出点D的坐标,并判断四边形ACBD的形状.
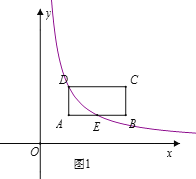
(3)如图2,将△ABD沿y轴的正方形以每秒1个单位长度的速度平移,得到△A′B′D′,A′B′与BC交于点E,A′D′与AB交于点F.连接EF,AB′,EF与AB′交于点G.设运动的时间为t(0≤t≤2)秒.
①当直线EF经过抛物线的顶点T时,请求出此时t的值;
②请直接写出点G经过的路径的长.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)D(3,﹣2).四边形ACBD是矩形,理由见解析;(3)①t的值为
x+2;(2)D(3,﹣2).四边形ACBD是矩形,理由见解析;(3)①t的值为![]() ;②点G经过的路径的长为1.
;②点G经过的路径的长为1.
【解析】
(1)将A点和B点坐标代入y=ax2+bx+2得a、b的方程组,解此方程组即可得答案,
(2)先利用勾股定理的逆定理证明△ACB为直角三角形,∠ACB=90°,根据△ABD与△ABC全等可知AC=BD,BC=AD,则可证明四边形ABCD为矩形;过点D作DM⊥x轴于M,通过证明△COB≌△DMA,即可求出D点坐标,
(3)①利用二次函数的性质得到顶点T的坐标为(![]() );可得直线BC的解析式为y=﹣
);可得直线BC的解析式为y=﹣![]() x+2,直线AD的解析式为y= -
x+2,直线AD的解析式为y= -![]() x﹣
x﹣![]() ,利用直线的平移得到直线A′D′的解析式为y=﹣
,利用直线的平移得到直线A′D′的解析式为y=﹣![]() x﹣
x﹣![]() +t,直线A′B′的解析式为y=t,则F(2t﹣1,0),E(4﹣2t,t),接着利用待定系数法求出直线EF的解析式为y=
+t,直线A′B′的解析式为y=t,则F(2t﹣1,0),E(4﹣2t,t),接着利用待定系数法求出直线EF的解析式为y=![]() ,然后把T点坐标代入得到关于t的方程,然后解此方程即可;
,然后把T点坐标代入得到关于t的方程,然后解此方程即可;
②先求出直线AB′的解析式为y=![]() ,再解方程组
,再解方程组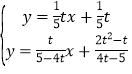 得G(
得G(![]() ),利用G点的坐标特征可判断点G在直线x=
),利用G点的坐标特征可判断点G在直线x=![]() ,然后利用0≤t≤2得到点G经过的路径的长
,然后利用0≤t≤2得到点G经过的路径的长
(1)将A(﹣1,0),B(4,0)两点坐标代入y=ax2+bx+2得![]() ,解得
,解得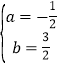 ,
,
∴抛物线的表达式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)D(3,﹣2).四边形ACBD是矩形,理由如下:
当x=0时,得y=2,
∴OC=2,由A(﹣1,0),B(4,0)得OA=1,OB=4.
∴AC2=12+22=5,BC2=22+42=20,AB2=52=25,
∴AC2+BC2=AB2,
∴△ACB为直角三角形,∠ACB=90°,
∵△ABD与△ABC全等,
∴AC=BD,BC=AD,
∴四边形ABCD为平行四边形,
而∠ACB=90°,
∴四边形ABCD为矩形.
如图,过点D作DM⊥x轴于M,
∵∠COB=∠AMD=90°,∠CBA=∠DAB,BC=AD,
∴△COB≌△DMA,
∴AM=OB,OC=DM=2,
∴OM=AM-1=OB-1=3
∴D(3,-2)
(3)①∵y=﹣![]() x2+
x2+![]() x+2=﹣
x+2=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴顶点T的坐标为(![]() );
);
∵B(4,0) , C(0,2), A(-1,0) D(3,-2)
∴直线BC的解析式为y=﹣![]() x+2,直线AD的解析式为y=﹣
x+2,直线AD的解析式为y=﹣![]() x﹣
x﹣![]() ,
,
∵直线AD向上平移t个单位得到A′D′,直线AB向上平移t个单位得到A′B′,
∴直线A′D′的解析式为y=﹣![]() x﹣
x﹣![]() +t,直线A′B′的解析式为y=t,
+t,直线A′B′的解析式为y=t,
当y=0时,﹣![]() x﹣
x﹣![]() +t=0,解得x=2t﹣1,则F(2t﹣1,0),
+t=0,解得x=2t﹣1,则F(2t﹣1,0),
当y=t时,﹣![]() x+2=t,解得x=4﹣2t,则E(4﹣2t,t),
x+2=t,解得x=4﹣2t,则E(4﹣2t,t),
设直线EF的解析式为y=mx+n,
把E(4﹣2t,t),F(2t﹣1,0)代入得![]() ,解得
,解得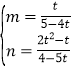 ,
,
∴直线EF的解析式为y=![]() ,
,
把T(![]() )代入得
)代入得![]() ,
,
整理得16t2﹣120t+125=0,解得t1=![]() ,t2=
,t2=![]() (舍去),
(舍去),
∴此时t的值为![]() ;
;
②∵直线AB向上平移t个单位得到A′B′,
∴B′(4,t),
易得直线AB′的解析式为y=![]() tx+
tx+![]() t,
t,
解方程组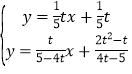 得
得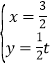 ,则G(
,则G(![]() ),
),
∴点G的横坐标为定值,点G在直线x=![]() 上,
上,
而0≤t≤2,
∴点G经过的路径的长为1.

 发散思维新课堂系列答案
发散思维新课堂系列答案