题目内容
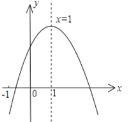
【题目】已知:抛物线C1:y=ax2+bx+c经过点A(-1,0)、B(3,0)、C(0,-3).
(1)求抛物线C1的解析式;
(2)将抛物线C1向左平移几个单位长度,可使所得的抛物线C2经过坐标原点,并求出C2的解析式;
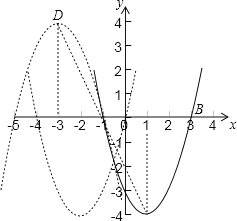
(3)把抛物线C1绕点A(-1,O)旋转180°,写出所得抛物线C3顶点D的坐标.
【答案】(1)抛物线C1:![]() (2)向左平移3个单位长度抛物线C2:
(2)向左平移3个单位长度抛物线C2:![]() ;(3)(-3,4).
;(3)(-3,4).
【解析】
(1)根据y=ax2+bx+c经过点A(-1,0)、B(3,0)、C(0,-3)列出三元一次方程,解得a、b、c;
(2)求出原函数的图象对称轴,然后运用平移知识解答;
(3)根据旋转的知识点,求出D点坐标.
(1)∵y=ax2+bx+c经过点A(-1,0)、B(3,0)、C(0,-3).
∴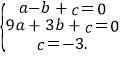
解得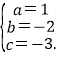
∴所求抛物线C1的解析式为:y=x2-2x-3;
(2)抛物线C1向左平移3个单位长度,可使得到的抛物线C2经过坐标原点
所求抛物线C2的解析式为:y=x(x+4)=x2+4x;
(3)D点的坐标为(-3,4).

 名校名卷单元同步训练测试题系列答案
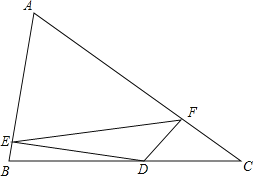
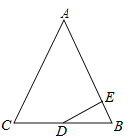
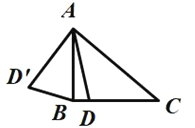
名校名卷单元同步训练测试题系列答案【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的动点,将线段
上的动点,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() 为
为![]() ,
,![]() 为
为![]() .
.
小明根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究,下面是小明的探究过程.请补充完整(说明:解答中所填数值均保留一位小数)
的变化而变化的规律进行了探究,下面是小明的探究过程.请补充完整(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 |
| 0.7 | 0.9 | 1.1 |
![]() 的值约为____________;
的值约为____________;
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图像.

(3)结合画出的函数图像,解决问题:
①线段![]() 的长度的最小值约为____________
的长度的最小值约为____________![]() ;
;
②![]() ,则
,则![]() 的长度
的长度![]() 的取值范围是____________.
的取值范围是____________.