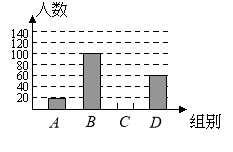ЬтФПФкШн
ЁОЬтФПЁПФГВшвЖЯњЪлЩЬМЦЛЎНЋmЙоВшвЖАДМзЁЂввСНжжРёЦЗКаАќзАГіЪлЃЌЦфжаМзжжРёЦЗКаУПКазА4ЙоЃЌУПКаЪлМл240дЊЃЛввжжРёЦЗКаУПКазА6ЙоЃЌУПКаЪлМл300дЊЃЌЧЁКУШЋВПзАЭъ.вбжЊУПЙоВшвЖЕФГЩБОМлЮЊ30дЊЃЌЩшМзжжРёЦЗКаЕФЪ§СПЮЊxКаЃЌввжжРёЦЗКаЕФЪ§СПЮЊyКа.
(1)ЕБm=120ЪБ.
ЂйЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪН.
ЂкШє120ЙоВшвЖШЋВПЪлГіКѓЕФзмРћШѓВЛЕЭгк3000дЊЃЌдђМзжжРёЦЗКаЕФЪ§СПжСЩйвЊЖрЩйКаЃП
(2)ШєmЙоВшвЖШЋВПЪлГіКѓЦНОљУПЙоЕФРћШѓЧЁКУЮЊ24дЊЃЌЧвМзЁЂввСНжжРёЦЗКаЕФЪ§СПКЭВЛГЌЙ§69КаЃЌЧѓmЕФзюДѓжЕ.
ЁОД№АИЁПЃЈ1ЃЉЂйy=-![]() x+20ЃЛЂкМзжжРёЦЗКаЕФЪ§СПжСЩйвЊ15КаЃЛ(2)340.
x+20ЃЛЂкМзжжРёЦЗКаЕФЪ§СПжСЩйвЊ15КаЃЛ(2)340.
ЁОНтЮіЁП
ЃЈ1ЃЉЂйИљОнСНжжРёКаЙВзА120ЙоСаЗНГЬМДПЩЃЛЂкИљОнЬтвтСаВЛЕШЪНЃЌЧѓГіxЕФШЁжЕЗЖЮЇМДПЩЕФД№АИЃЛЃЈ2ЃЉИљОнЬтвтСаЗНГЬзщЃЌПЩЕУx=y,НјЖјПЩЕУm=10xЃЌИљОнx+yЁм69,xЪЧећЪ§ПЩЕУxЕФзюДѓжЕЃЌМДПЩЧѓГіmЕФзюДѓжЕ.
ЃЈ1ЃЉгЩЬтвтЃЌЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
ЃЈ2ЃЉгЩЬтвтЃЌЕУ![]() ЃЌгж
ЃЌгж![]() ЃЌ
ЃЌ
Ёр![]() ЃЌНтЕУxЁн15ЃЌ
ЃЌНтЕУxЁн15ЃЌ
ЁрМзжжРёЦЗКаЕФЪ§СПжСЩйвЊ15КаЃЌЗћКЯЬтвт.
ЃЈ3ЃЉгЩЬтвтЃЌЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрx=yЃЌm=10xЃЌ
гж![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
вђЮЊxЪЧећЪ§ЃЌЫљвдxЕФзюДѓжЕЮЊ34ЃЌ
ЁрmЕФзюДѓжЕЮЊ340.

 аЁбЇЩњ10ЗжжгПкЫуВтЪд100ЗжЯЕСаД№АИ
аЁбЇЩњ10ЗжжгПкЫуВтЪд100ЗжЯЕСаД№АИ