题目内容
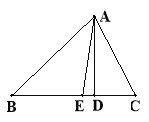
【题目】在△ABC中，AB=AC，∠ABC=90°，D为AC中点，点P是线段AD上的一点，点P与点A，点D不重合），连接BP．将△ABP绕点P按顺时针方向旋转α角（0°＜α＜180°），得到△A1B1P，连接A1B1、BB1
（1）如图①，当0°＜α＜90°，在α角变化过程中，请证明∠PAA1=∠PBB2 ．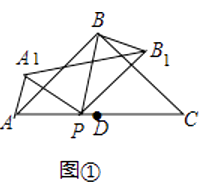 
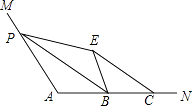
（2）如图②，直线AA1与直线PB、直线BB1分别交于点E，F．设∠ABP=β，当90°＜α＜180°时，在α角变化过程中，是否存在△BEF与△AEP全等？若存在，求出α与β之间的数量关系；若不存在，请说明理由；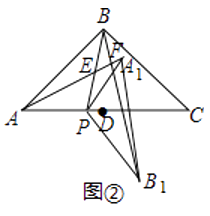
（3）如图③，当α=90°时，点E、F与点B重合．直线A1B与直线PB相交于点M，直线BB′与AC相交于点Q．若AB= 
，设AP=x，求y关于x的函数关系式．
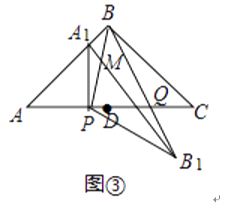
【答案】
（1）解：∵将△ABP绕点P按顺时针方向旋转α角（0°＜α＜180°），得到△A1B1P，
∴∠APA1=∠BPB1=α，AP=A1P，BP=B1P，
∴∠AA1P=∠A1AP= 
= 
，∠BB1P=∠B1BP= 
= ，
∴∠PAA1=∠PBB1
（2）解：假设在α角变化的过程中，存在△BEF与△AEP全等，
∵△BEF与△AEP全等，
∴AE=BE，
∴∠ABE=∠BAE=β，
∵AP=A1P，
∴∠A1AP=∠AA1P= ，
∵AB=BC，∠ABC=90°，
∴∠BAC=45°，
∴β+ =45°，
∴α﹣2β=90°
（3）解：当α=90°时，
∵AP=A1P，BP=B1P，∠APA1=∠BPB2=90°，
∴∠A=∠PBB1=45°，
∵∠A=∠C，∠AQB=∠C+∠QBC=45°+∠QBC=∠PBC，
∴△ABQ∽△CPB，
∴ 
，
∵AB= 
，
∴ 
，
∴y= 
【解析】（1）将△ABP绕点P按顺时针方向旋转α角（0°＜α＜180°），得到△A1B1P，根据旋转的性质得到对应角相等对应边相等，求∠PAA1=∠PBB2；（2）在α角变化的过程中，存在△BEF与△AEP全等，得到对应角相等对应边相等，根据三角形内角和定理求出α﹣2β的值；（3）当α=90°时，根据旋转的性质得到△ABQ∽△CPB，求出比例，得到AB的值，求出y关于x的函数关系式.
【考点精析】本题主要考查了函数关系式的相关知识点，需要掌握用来表示函数关系的数学式子叫做函数解析式或函数关系式才能正确解答此题．
