题目内容
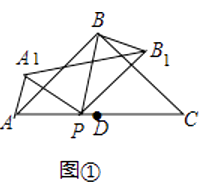
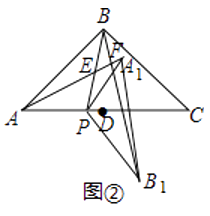
【题目】如图,顶点为A的抛物线y=a(x+2)2﹣4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.
(1)求抛物线的解析式;
(2)若动点P从点O出发,以每秒1个单位长度的速度沿着射线OM运动,设点P运动的时间为t秒,问:当t为何值时,OB=AP;
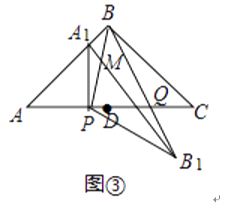
(3)若动点P从点O出发,以每秒1个单位长度的速度沿线段OD向点D运动,同时动点Q从点C出发,以每秒2个单位长度的速度沿线段CO向点O运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动时间为t秒,连接PQ.问:当t为何值时,四边形CDPQ的面积最小?并求此时PQ的长.
【答案】
(1)解:把(1,0)代入y=a(x+2)2﹣4,
得a= ![]() .
.
∴y= ![]() (x+2)2﹣4,
(x+2)2﹣4,
即y= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]()
(2)解:由题意得OP=t,AB= ![]() =5,
=5,
若OB∥AP,即四边形ABOP为平行四边形时,OB=AP,且OP=AB=5,即当t=5时,OB=AP,
若OB不平行于AP,即四边形ABOP为等腰梯形时,OB=AP,连接AP,过点P作PG⊥AB,过点O作OH⊥AB,垂足分别为G、H,
∴△APG≌△BOH,
在Rt△OBM中,
∵OM= ![]() ,OB=1,
,OB=1,
∴BM= ![]() ,
,
∴OH= ![]() ,
,
∴BH= ![]() ,
,
∴OP=GH=AB﹣2BH= ![]() ,
,
即当t= ![]() 时,OB=AP
时,OB=AP
(3)解:将y=0代入y= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() ,得
,得 ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() =0,
=0,
解得x=1或﹣5.
∴C(﹣5,0).
∴OC=5,
∵OM∥AB,AD∥x轴,
∴四边形ABOD是平行四边形,
∴AD=OB=1,
∴点D的坐标是(﹣3,﹣4),
∴S△DOC= ![]() ×5×4=10,
×5×4=10,
过点P作PN⊥BC,垂足为N.易证△OPN∽△BOH,

∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴PN= ![]() t,
t,
∴四边形CDPQ的面积S=S△DOC﹣S△OPQ=10﹣ ![]() ×(5﹣2t)×
×(5﹣2t)× ![]() t=
t= ![]() t2﹣2t+10,
t2﹣2t+10,
∴当t= ![]() 时,四边形CDPQ的面积S最小,
时,四边形CDPQ的面积S最小,
此时,点P的坐标是(﹣ ![]() ,﹣1),点Q的坐标是(﹣
,﹣1),点Q的坐标是(﹣ ![]() ,0),
,0),
∴PQ= ![]() =
= ![]() .
.
【解析】(1)把点B(1,0)代入抛物线的解析式,求出抛物线的解析式;(2)根据勾股定理求出AB的值,若OB∥AP,即四边形ABOP为平行四边形时,OB=AP,且OP=AB,当t=5时,OB=AP;若OB不平行于AP,即四边形ABOP为等腰梯形时,OB=AP,得到△APG≌△BOH,在Rt△OBM中,求出
BM![]() ,OH
,OH![]() ,BH
,BH![]() 的值,OP=GH=AB﹣2BH的值即可;(3)根据题意求出C的坐标,得到OC的值,由OM∥AB,AD∥x轴,得到四边形ABOD是平行四边形,AD=OB,求出点D的坐标,求出S△DOC的面积 ,证出△OPN∽△BOH,得到比例,求出PN的值,得到四边形CDPQ的面积S=S△DOC﹣S△OPQ,求出PQ的值;此题是综合题,难度较大,计算和解方程时需认真仔细.
的值,OP=GH=AB﹣2BH的值即可;(3)根据题意求出C的坐标,得到OC的值,由OM∥AB,AD∥x轴,得到四边形ABOD是平行四边形,AD=OB,求出点D的坐标,求出S△DOC的面积 ,证出△OPN∽△BOH,得到比例,求出PN的值,得到四边形CDPQ的面积S=S△DOC﹣S△OPQ,求出PQ的值;此题是综合题,难度较大,计算和解方程时需认真仔细.

 名校课堂系列答案
名校课堂系列答案【题目】某校在艺术节宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
选项 | 方式 | 百分比 |
A | 唱歌 | 35% |
B | 舞蹈 | a |
C | 朗诵 | 25% |
D | 器乐 | 30% |
请结合统计图表,回答下列问题: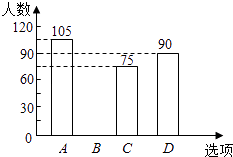
(1)本次调查的学生共人,a= , 并将条形统计图补充完整 ;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式有一种是“唱歌”的概率.