Question

【题目】如图，在△ABC中，AE是∠BAC的角平分线，AD是BC边上的高，且∠B ＝ 40, ∠C ＝ 60,求∠CAD、∠EAD的度数。（6分）

Answer 1

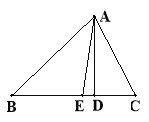
【答案】解：∵AD是BC边上的高，∠C=60°，

∴∠CAD=90°-∠C=90°-60°=30°；

在△ABC中，∠BAC=180°-∠B-∠C=180°-40°-60°=80°，

∵AE是∠BAC的角平分线，

∴∠CAE=∠BAC=×80°=40°，

∴∠EAD=∠CAE-∠CAD=40°-30°=10°．

【解析】

试题根据直角三角形两锐角互余可得∠CAD=90°-∠C，再利用三角形的内角和定理求出∠BAC，根据角平分线的定义求出∠CAE，然后根据∠EAD=∠CAE-∠CAD计算即可得解．∴∠EAD=∠CAE-∠CAD=40°-30°=10°．