题目内容
【题目】在
中，
是
的中点，
，
分别是
的三等分点，
，
分别交
于
，
两点，则
等于（ ）
A. 3:2:1 B. 4:2:1 C. 5:2:1 D. 5:3:2
【答案】D
【解析】
如图，作PD∥BC，QE∥AC，由D为AC的中点，可得PD：FC=1：2，再由E，F为BC边三等分点，可求得PD：BF=1：4，即可求出DN：NB=PD：BF=1：4，所以ND=
BD，然后再根据BQ：QD=QE：CD=BE：BC=1：3，求得BQ=
BD，QM=
BD，继而推出BM与BD的关系，由此即可解答．
如图，作PD∥BC，QE∥AC，
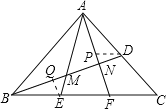
∵D为AC的中点，
∴PD：FC=1：2，
∵E，F为BC边三等分点，
∴PD：BF=1：4，
∴DN：NB=PD：BF=1：4，
∴ND=BD，BQ：QD=QE：CD=BE：BC=1：3，
∴BQ=BD，QM=
QD=×
BD=BD，
∴BM=BQ+QM=
BD，
∴BM：MN：ND=5：3：2．
故选D．
练习册系列答案
相关题目
