Question

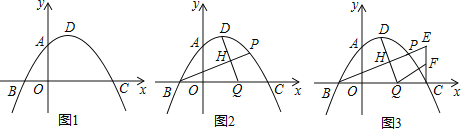
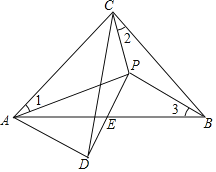
【题目】如图，在等腰直角三角形ABC中，∠ACB＝90°，在△ABC内一点P，已知∠1＝∠2＝∠3，将△BCP以直线PC为对称轴翻折，使点B与点D重合，PD与AB交于点E，连结AD，将△APD的面积记为S1，将△BPE的面积记为S2，则的值为_____．

Answer 1

【答案】

【解析】

首先证明∠APC＝90°，∠BPC＝∠APB＝∠ADB＝135°，再证明△PDB，△ADP都是等腰直角三角形即可解决问题．

如图，连接BD．

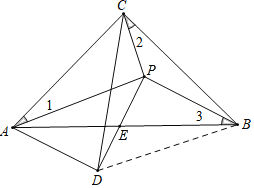
∵CA＝CB，∠ACB＝90°，

∴∠CAB＝∠CBA＝45°，

∵∠1＝∠2，∠2+∠ACP＝90°，

∴∠1+∠ACP＝90°，

∴∠APC＝90°，

∵∠2＝∠3，∠3+∠PBC＝45°，

∴∠2+∠PBC＝45°，

∴∠BPC＝∠DPC＝135°，

∴∠APD＝45°，∠DPB＝90°，

∵PD＝PB，

∴△PDB是等腰直角三角形，

同法可知：∠APB＝135°，

∴∠APD＝45°，

∵CA＝CD＝CB，

∴∠CAD＝∠CDA，∠CDB＝∠CBD，

∵∠ACD+2∠CDA＝180°，∠DCB+2∠CDB＝180°，∠ACD+∠DCB＝90°，

∴2∠ADC+2∠CDB＝270°，

∴∠ADP＝∠ADC+∠CDB＝135°，

∵∠PDB＝45°，

∴∠ADP＝90°，

∵∠APD＝45°，

∴△APD是等腰直角三角形，

∴AD＝PD＝PB，

∵∠ADP＝∠DPB＝90°，

∴AD∥PB，

∴四边形ADBP是平行四边形，

∴PE＝DE，

∴S2＝S△DPBS△ADP＝S1．

∴＝，

故答案为．