题目内容
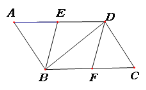
【题目】如图,已知ABCD,点E是BC边上的一点,将边AD延长至点F,使∠AFC=∠DEC.

(1)求证:四边形DECF是平行四边形;
(2)若AB=13,DF=14,tan A=![]() ,求CF的长.
,求CF的长.
【答案】(1)见解析;(2)15
【解析】 试题分析:(1)由已知可知AD∥BC,从而得∠ADE=∠DEC,再根据∠AFC=∠DEC,从而得∠AFC=∠ADE,继而得DE∥FC,问题得证;
(2)过点D作DH⊥BC于点H,由已知得到∠BCD=∠A,AB=CD=13,再根据tan A=tan∠DCH=![]() ,从而得到DH、CH的长,从而得到CE、DE的长,继而得CF的长.
,从而得到DH、CH的长,从而得到CE、DE的长,继而得CF的长.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠ADE=∠DEC,
又∵∠AFC=∠DEC,∴∠AFC=∠ADE,
∴DE∥FC,
∴四边形DECF是平行四边形;
(2)过点D作DH⊥BC于点H,如图所示.
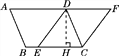
∵四边形ABCD是平行四边形,
∴∠BCD=∠A,AB=CD=13,
又∵tan A=![]() =tan∠DCH=
=tan∠DCH=![]() ,
,
∴DH=12,CH=5,
∵DF=14,∴CE=14,
∴EH=9,
∴DE=![]() =15,
=15,
∴CF=DE=15.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目