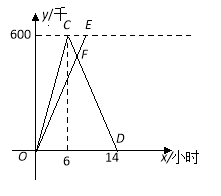
Ő‚ńŅńŕ»›
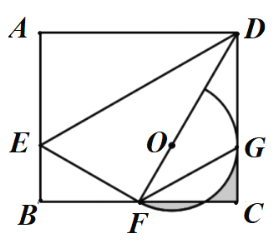
°ĺŐ‚ńŅ°Ņ‘ŕ≥ű÷–Ĺ◊∂őĶńļĮ ż—ßŌį÷–£¨ő“√«ĺ≠ņķŃňŃ–ĪŪ°Ę√ŤĶ„°ĘѨŌŖĽ≠ļĮ żÕľŌů£¨≤ĘĹŠļŌÕľŌů—–ĺŅļĮ ż–‘÷ ĶńĻż≥Ő£ģ“‘Ō¬ «ő“√«—–ĺŅļĮ ż![]() –‘÷ ľį∆š”¶”√Ķń≤Ņ∑÷Ļż≥Ő£¨«Žįī“™«ůÕÍ≥…Ō¬Ń–łų–°Ő‚£ģ
–‘÷ ľį∆š”¶”√Ķń≤Ņ∑÷Ļż≥Ő£¨«Žįī“™«ůÕÍ≥…Ō¬Ń–łų–°Ő‚£ģ
£®1£©«Žį—Ō¬ĪŪ≤Ļ≥šÕÍ’Ż£¨≤Ę‘ŕÕľ÷–≤Ļ»ęł√ļĮ żÕľŌů£Ľ
| °≠ | £≠5 | £≠4 | £≠3 | £≠2 | £≠1 | 0 | 1 | 2 | 3 | 4 | 5 | °≠ |
| °≠ |
|
|
| £≠3 | 0 | 3 |
|
|
| °≠ |
£®2£©łýĺ›ļĮ żÕľŌů£¨Ň–∂ŌŌ¬Ń–Ļō”ŕł√ļĮ ż–‘÷ ĶńňĶ∑® «∑Ů’ż»∑£¨’ż»∑Ķń‘ŕŌŗ”¶Ķńņ®ļŇńŕīÚ°į°Ő°Ī£¨īŪőůĶń‘ŕŌŗ”¶Ķńņ®ļŇńŕīÚ°į°Ń°Ī£Ľ
ĘŔł√ļĮ żÕľŌů «÷Š∂‘≥∆Õľ–ő£¨ňŁĶń∂‘≥∆÷Šő™y÷Š£Ľ( )
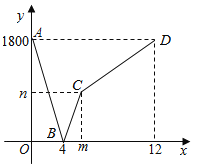
Ęŕł√ļĮ ż‘ŕ◊‘ĪšŃŅĶń»°÷Ķ∑∂őßńŕ£¨”–◊Óīů÷ĶļÕ◊Ó–°÷Ķ£¨ĶĪ![]() Ī£¨ļĮ ż»°Ķ√◊Óīů÷Ķ3£ĽĶĪ
Ī£¨ļĮ ż»°Ķ√◊Óīů÷Ķ3£ĽĶĪ![]() Ī£¨ļĮ ż»°Ķ√◊Ó–°÷Ķ£≠3£Ľ( )
Ī£¨ļĮ ż»°Ķ√◊Ó–°÷Ķ£≠3£Ľ( )
ĘŘĶĪ![]() ĽÚ
ĽÚ![]() Ī£¨yňśxĶń‘Ųīů∂Ýľű–°£ĽĶĪ
Ī£¨yňśxĶń‘Ųīů∂Ýľű–°£ĽĶĪ![]() Ī£¨yňśxĶń‘Ųīů∂Ý‘Ųīů£Ľ( )
Ī£¨yňśxĶń‘Ųīů∂Ý‘Ųīů£Ľ( )
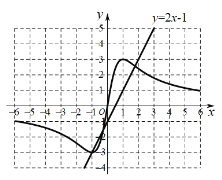
£®3£©“—÷™ļĮ ż![]() ĶńÕľŌů»ÁÕľňý ĺ£¨ĹŠļŌń„ňýĽ≠ĶńļĮ żÕľŌů£¨÷ĪĹ”–ī≥Ų≤ĽĶ» Ĺ
ĶńÕľŌů»ÁÕľňý ĺ£¨ĹŠļŌń„ňýĽ≠ĶńļĮ żÕľŌů£¨÷ĪĹ”–ī≥Ų≤ĽĶ» Ĺ![]() ĶńĹ‚ľĮ£®Ī£ŃŰ1őĽ–° ż£¨őů≤Ó≤Ľ≥¨Ļż0.2£©£ģ
ĶńĹ‚ľĮ£®Ī£ŃŰ1őĽ–° ż£¨őů≤Ó≤Ľ≥¨Ļż0.2£©£ģ

°ĺīūįł°Ņ£®1£©![]() £¨
£¨![]() £Ľ£®2£©ĘŔ°Ń Ęŕ°Ő ĘŘ°Ő£Ľ£®3£©x£ľ1ĽÚ0.3£ľx£ľ1.8£ģ
£Ľ£®2£©ĘŔ°Ń Ęŕ°Ő ĘŘ°Ő£Ľ£®3£©x£ľ1ĽÚ0.3£ľx£ľ1.8£ģ
°ĺĹ‚őŲ°Ņ
£®1£©īķ»Žx=3ļÕx=-3ľīŅ…«ů≥Ų∂‘”¶Ķńy÷Ķ£¨‘Ŕ≤Ļ»ęļĮ żÕľŌůľīŅ…£Ľ
£®2£©ĹŠļŌļĮ żÕľŌůŅ…ī”‘Ųľű–‘ľį∂‘≥∆–‘ĹÝ––Ň–∂Ō£Ľ
£®3£©łýĺ›ÕľŌů«ůĹ‚ľīŅ…£ģ
Ĺ‚£ļ£®1£©ĶĪx=-3 Ī£¨![]()
![]() £¨
£¨
ĶĪx=3 Ī£¨![]()
![]() £¨
£¨
ļĮ żÕľŌů»ÁŌ¬£ļ
£®2£©ĘŔ”…ļĮ żÕľŌůŅ…Ķ√ňŁ «÷––ń∂‘≥∆Õľ–ő£¨≤Ľ «÷Š∂‘≥∆Õľ–ő£Ľ
Ļ īūįłő™£ļ°Ń £¨
ĘŕĹŠļŌļĮ żÕľŌůŅ…Ķ√£ļł√ļĮ ż‘ŕ◊‘ĪšŃŅĶń»°÷Ķ∑∂őßńŕ£¨”–◊Óīů÷ĶļÕ◊Ó–°÷Ķ£¨ĶĪ![]() Ī£¨ļĮ ż»°Ķ√◊Óīů÷Ķ3£ĽĶĪ
Ī£¨ļĮ ż»°Ķ√◊Óīů÷Ķ3£ĽĶĪ![]() Ī£¨ļĮ ż»°Ķ√◊Ó–°÷Ķ£≠3£Ľ
Ī£¨ļĮ ż»°Ķ√◊Ó–°÷Ķ£≠3£Ľ
Ļ īūįłő™£ļ°Ő £¨
ĘŘĻŘ≤žļĮ żÕľŌůŅ…Ķ√£ļĶĪ![]() ĽÚ
ĽÚ![]() Ī£¨yňśxĶń‘Ųīů∂Ýľű–°£ĽĶĪ
Ī£¨yňśxĶń‘Ųīů∂Ýľű–°£ĽĶĪ![]() Ī£¨yňśxĶń‘Ųīů∂Ý‘Ųīů£Ľ
Ī£¨yňśxĶń‘Ųīů∂Ý‘Ųīů£Ľ
Ļ īūįłő™£ļ°Ő£ģ
£®3£©![]() £¨
£¨![]()
![]() Ī£¨
Ī£¨![]()
Ķ√![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
Ļ ł√≤ĽĶ» ĹĶńĹ‚ľĮő™£ļ x£ľ1ĽÚ0.3£ľx£ľ1.8£ģ