题目内容
19. 如图,在平面直角坐标系中,点B坐标为(1,-1),点C坐标为(4,0),以BC为边在BC的上方作一个正方形ABCD,点A在y轴上,过点A,B,C作一条抛物线.
如图,在平面直角坐标系中,点B坐标为(1,-1),点C坐标为(4,0),以BC为边在BC的上方作一个正方形ABCD,点A在y轴上,过点A,B,C作一条抛物线.(1)在线段BC下方的抛物线上是否存在点P,使S△BCP的面积最大?若不存在,说明理由;若存在,直接写出点P坐标.
(2)把抛物线向上平移m(m>0)个单位,使得抛物线始终与正方形ABCD的边有4个交点,直接写出m的取值范围.
分析 (1)作辅助线,构建全等三角形,如图1,证明△AEB≌△BFC,得出点A的坐标,利用待定系数法求抛物线和BC的解析式,因为点P在抛物线上,所以设P(m,$\frac{5}{6}$m2-$\frac{23}{6}$m+2),则H(m,$\frac{1}{3}$m-$\frac{4}{3}$),表示出PH的长,根据三角形面积=铅直高度×水平宽度,代入可表示出面积,利用配方法求最值,并计算点P的坐标;
(2)设平移后的抛物线的解析式为:y=$\frac{5}{6}$x2-$\frac{23}{6}$x+2+m,作出三个点到四个交点的界限,如图3,当平移后的抛物线与BC有一个交点时,此时与正方形有三个交点,列方程组计算△=0,此时m=$\frac{15}{8}$,观察图形发现当抛物线开始位置时与正方形也有三个交点,向上平移则开始有四个交点,由此写出m的取值.
解答  解:(1)如图1,过B作BE⊥y轴于E,过C作CF⊥BE于F,
解:(1)如图1,过B作BE⊥y轴于E,过C作CF⊥BE于F,
则∠AEB=∠BFC=90°,
∴∠EAB+∠ABE=90°,
∵点B坐标为(1,-1),点C坐标为(4,0),
∴BE=1,FC=OE=1,BF=4-1=3,
∵四边形ABCD为正方形,
∴∠ABC=90°,AB=BC,
∴∠ABE+∠FBC=90°,
∴∠EAB=∠FBC,
∴△AEB≌△BFC,
∴AE=BF=3,
∴OA=AE-OE=3-1=2,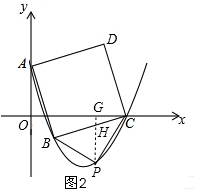
∴A(0,2),
设抛物线的解析式为:y=ax2+bx+c,
把B(1,-1),C(4,0),A(0,2)代入得:$\left\{\begin{array}{l}{a+b+c=-1}\\{16a+4b+c=0}\\{c=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{5}{6}}\\{b=-\frac{23}{6}}\\{c=2}\end{array}\right.$,
∴抛物线的解析式为:y=$\frac{5}{6}$x2-$\frac{23}{6}$x+2,
如图2,过P作PG⊥x轴于G,交BC于H,
设直线BC的解析式为:y=kx+b,
把B(1,-1),C(4,0)代入得:$\left\{\begin{array}{l}{k+b=-1}\\{4k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=-\frac{4}{3}}\end{array}\right.$,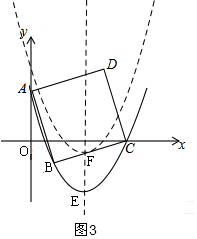
∴直线BC的解析式为:y=$\frac{1}{3}$x-$\frac{4}{3}$,
设P(m,$\frac{5}{6}$m2-$\frac{23}{6}$m+2),则H(m,$\frac{1}{3}$m-$\frac{4}{3}$),
∴PH=(-$\frac{5}{6}$m2+$\frac{23}{6}$m-2)-($\frac{4}{3}$-$\frac{1}{3}m$)=-$\frac{5}{6}{m}^{2}+\frac{25}{6}m-\frac{10}{3}$,
∴S△BPC=$\frac{1}{2}$PH•BF=$\frac{1}{2}$(-$\frac{5}{6}{m}^{2}+\frac{25}{6}m-\frac{10}{3}$)×3=-$\frac{5}{4}{m}^{2}+\frac{25}{4}m-5$=-$\frac{5}{4}$(m-$\frac{5}{2}$)2+$\frac{45}{16}$,
∵1<m<4,
∴当m=$\frac{5}{2}$时,S有最大值,
$\frac{5}{6}$m2-$\frac{23}{6}$m+2=$\frac{5}{6}$×$\frac{25}{4}$-$\frac{23}{6}$×$\frac{5}{2}$+2=-$\frac{19}{8}$,
∴当S△BCP的面积最大时,点P坐标为($\frac{5}{2}$,-$\frac{19}{8}$);
(2)设平移后的抛物线的解析式为:y=$\frac{5}{6}$x2-$\frac{23}{6}$x+2+m,
如图3,当平移后的抛物线与BC有一个交点时,此时与正方形有三个交点,
则$\left\{\begin{array}{l}{y=\frac{1}{3}x-\frac{4}{3}}\\{y=\frac{5}{6}{x}^{2}-\frac{23}{6}x+2+m}\end{array}\right.$,
∴$\frac{5}{6}$${m}^{2}-\frac{23}{6}m+2+m=\frac{1}{3}m-\frac{4}{3}$,
5x2-25x+20+6m=0,
△=(-25)2-4×5×(20+6m)=0,
m=$\frac{15}{8}$,
∴m的取值范围是0<m<$\frac{15}{8}$.
点评 本题考查了利用待定系数法求抛物线和一次函数的解析式、二次函数图象的平移问题、最值及正方形的性质,明确平移原则:上→加,下→减,知道求二次函数的最值有两种方法:①配方成顶点式,写出最值,②代入顶点坐标(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$);本题第2问有难度,是考查了函数与直线的交点问题,利用数形结合的方法解决比较简便.

 如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.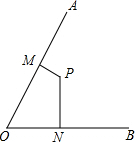 如图,∠AOB=60°,点P在∠AOB的内部,且点P到OA、OB的距离为a和b,且a<b,点M在OA上,点N在OB上,则PM+MN的最小值为a+b.
如图,∠AOB=60°,点P在∠AOB的内部,且点P到OA、OB的距离为a和b,且a<b,点M在OA上,点N在OB上,则PM+MN的最小值为a+b. 如图,一条抛物线经过(-2,5),(0,-3)和(1,-4)三点.
如图,一条抛物线经过(-2,5),(0,-3)和(1,-4)三点.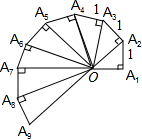 如图是第七届国际数学教育大会的会徽示意图,主题图案是由一连串如图所示的直角三角形演化而成的.其中的第一个三角形OA1A2是等腰直角三角形,且OA1=A1A2=A2A3…=A8A9=1.
如图是第七届国际数学教育大会的会徽示意图,主题图案是由一连串如图所示的直角三角形演化而成的.其中的第一个三角形OA1A2是等腰直角三角形,且OA1=A1A2=A2A3…=A8A9=1.