题目内容
9. 如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.(1)求证:△APQ∽△CDQ;
(2)若DP⊥AC,求AP的长.
分析 (1)根据矩形的性质可得CD∥AB,根据平行线的性质可得∠DCQ=∠QAP,∠PDC=∠QPA,进而可得判定△APQ∽△CDQ;
(2)首先证明△ADQ∽△ACD,根据相似三角形的性质可得 $\frac{AD}{AC}$=$\frac{AQ}{AD}$,然后计算出AC长,进而可得AQ长,再证明△AQP∽△ABC,可得 $\frac{AQ}{AP}$=$\frac{AB}{AC}$,由此解决问题.
解答 (1)证明:∵四边形ABCD是矩形,
∴CD∥AB,
∴∠DCQ=∠QAP,∠PDC=∠QPA,
∴△APQ∽△CDQ;
(2)解:∵∠ADC=90°,DP⊥AC,
∴∠AQD=∠AQP=∠ADC=90°,
∵∠DAQ=∠CAD,
∴△ADQ∽△ACD,
∴$\frac{AD}{AC}$=$\frac{AQ}{AD}$,
∵AC=$\sqrt{1{0}^{2}+2{0}^{2}}$=10$\sqrt{5}$,
则AQ=$\frac{A{D}^{2}}{AC}$═2 $\sqrt{5}$,
∵∠AQP=∠ABC=90°,∠QAP=∠BAC,
∴△AQP∽△ABC,
∴$\frac{AQ}{AP}$=$\frac{AB}{AC}$,
则 $\frac{2\sqrt{5}}{AP}$=$\frac{20}{10\sqrt{5}}$,
解得:AP=5,
点评 此题主要考查了相似三角形的判定和性质、勾股定理等知识,关键是掌握有两个角对应相等的三角形相似,灵活运用相似三角形的性质解决问题.

练习册系列答案
相关题目
 已知:抛物线C1的顶点坐标为(2,1),且经过(1,0).把C1先向左平移2个单位,再向上平移8个单位得到抛物线C2.
已知:抛物线C1的顶点坐标为(2,1),且经过(1,0).把C1先向左平移2个单位,再向上平移8个单位得到抛物线C2. 如图,E是正方形ABCD对角线BD上一点,EM⊥BC,EN⊥CD垂足分别是求M、N
如图,E是正方形ABCD对角线BD上一点,EM⊥BC,EN⊥CD垂足分别是求M、N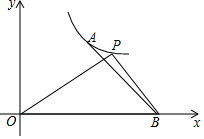 如图,已知反比例函数y=$\frac{k}{x}$(k≠0)图象经过点A(3,4),点B(6,0)在x轴正半轴上.
如图,已知反比例函数y=$\frac{k}{x}$(k≠0)图象经过点A(3,4),点B(6,0)在x轴正半轴上.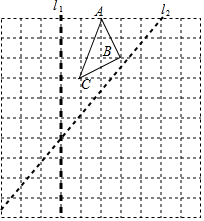 在图中先画出△ABC关于直线l1的轴对称图形△A1B1C1,再画出△A1B1C1关于直线l2的轴对称图形△A2B2C2.
在图中先画出△ABC关于直线l1的轴对称图形△A1B1C1,再画出△A1B1C1关于直线l2的轴对称图形△A2B2C2. 如图,在平面直角坐标系中,点B坐标为(1,-1),点C坐标为(4,0),以BC为边在BC的上方作一个正方形ABCD,点A在y轴上,过点A,B,C作一条抛物线.
如图,在平面直角坐标系中,点B坐标为(1,-1),点C坐标为(4,0),以BC为边在BC的上方作一个正方形ABCD,点A在y轴上,过点A,B,C作一条抛物线.