题目内容
【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果BE=10,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.

【答案】(1)详见解析;(2)30°;(3)![]() .
.
【解析】试题分析:(1)连接![]() 圆的半径相等和已知条件证明
圆的半径相等和已知条件证明![]() ,即可证明
,即可证明![]() 是
是![]() 的切线;
的切线;
(2)连接![]() 首先证明
首先证明![]() 是等边三角形,再利用圆周角定理:同弧所对的圆周角是所对圆心角的一半即可求出∠
是等边三角形,再利用圆周角定理:同弧所对的圆周角是所对圆心角的一半即可求出∠![]() 的度数;
的度数;
(3)过点O作OG⊥AB于点G,得到AG=BG,在![]() 中
中![]() 设DE=5x,则AE=13x,AD=12x,AO=24x,把
设DE=5x,则AE=13x,AD=12x,AO=24x,把![]() 表示出来,在
表示出来,在![]() 中,用三角函数的知识列出方程,解出
中,用三角函数的知识列出方程,解出![]() 得值,即可求出半径.
得值,即可求出半径.
试题解析:(1)证明:连接OB,
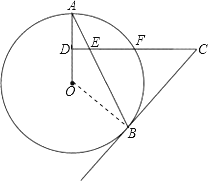
∵OB=OA,CE=CB,
∴∠A=∠OBA,∠CEB=∠ABC.
又∵CD⊥OA.
![]()
![]()
∴OB⊥BC
∴BC是![]() 的切线.
的切线.
(2)连接OF,AF,BF,
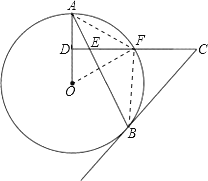
∵DA=DO,CD⊥OA,
∴AF=OF,
∵OA=OF,
∴△OAF是等边三角形,
![]()
![]()
(3)连接OF,AF,
∵DA=
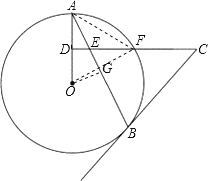
∴AF=OF=OA,
过点O作OG⊥AB于点G,得到AG=BG,
在![]() 中
中![]()
设DE=5x,则AE=13x,AD=12x,AO=24x,
∵BE=10,∴AB=10+13x.
则![]()
又∵![]() 中,
中, ![]() 则
则![]()
则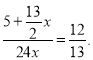
解得![]()
![]()

练习册系列答案
相关题目