题目内容
【题目】如图是作一个角的角平分线的方法:以![]() 的顶点
的顶点![]() 为圆心,以任意长为半径画弧,分别交
为圆心,以任意长为半径画弧,分别交![]() 于
于![]() 两点,再分别以
两点,再分别以![]() 为圆心,大于
为圆心,大于![]() 长为半径作画弧,两条弧交于点
长为半径作画弧,两条弧交于点![]() ,作射线
,作射线![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.

(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,垂足为
,垂足为![]() ,求证:
,求证:![]() .
.
【答案】(1)35°;(2)见解析.
【解析】
(1)首先根据OB∥FD,可得∠OFD+∠AOB=18O°,进而得到∠AOB的度数,再根据作图可知OP平分∠AOB,进而算出∠DOB的度数即可;
(2)首先证明∴∠AOD=∠ODF,再由FM⊥OD可得∠OMF=∠DMF,再加上公共边FM=FM,可利用AAS证明△FMO≌△FMD.
(1)解:∵OB∥FD,
∴∠OFD+∠AOB=18O°,
又∵∠OFD=110°,
∴∠AOB=180°∠OFD=180°110°=70°,
由作法知,OP是∠AOB的平分线,
∴∠DOB=![]() ∠ABO=
∠ABO=![]() ;
;
(2)证明:∵OP平分∠AOB,
∴∠AOD=∠DOB,
∵OB∥FD,
∴∠DOB=∠ODF,
∴∠AOD=∠ODF,
又∵FM⊥OD,
∴∠OMF=∠DMF,
在△MFO和△MFD中
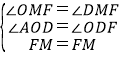
∴△MFO≌△MFD(AAS).

练习册系列答案
相关题目
【题目】一名同学调查了全班![]() 名同学分别喜欢相声、小品、歌曲、舞蹈节目的类别情况,并制成如下统计表:
名同学分别喜欢相声、小品、歌曲、舞蹈节目的类别情况,并制成如下统计表:
最喜欢的节目类别 | 划记 | 人数 | 百分数(%) |
相声 | 正 |
|
|
小品 | 正正正一 |
|
|
歌曲 | 正正 |
|
|
舞蹈 | 正一 |
|
|
其中对这些节目类别的统计中,仅有一类节目的统计是完全正确的,该项统计类别是( )
A.相声B.小品C.歌曲D.舞蹈


