Question

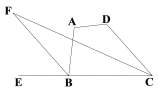
【题目】把一张矩形纸片ABCD按如图方式折叠，使点A与点E重合，点C与点F重合（E，F两点均在BD上），折痕分别为BH，DG．

（1）求证：BH∥DG；

（2）求证：△BEH≌△DFG；

（3）若AB=6 cm，BC=8 cm．

①BF=________cm；

②求线段CG的长．

Answer 1

【答案】（1）见解析；（2）见解析；（3）① 4；②CG=3 cm

【解析】

（1）根据折叠的性质可得，再根据平行线的性质得到∠1=∠2，故可求解；

（2）根据矩形的性质及ASA即可证明△BEH≌△DFG；

（3）①先根据勾股定理求出BD，再得到DF=CD=8,即可求出BF的长；

②由图形翻折变换的性质得出CG＝FG，设CG＝x，则BG＝8x，再利用勾股定理即可求出x的值．

解：（1）由折叠可知：．

在矩形ABCD中，AB//CD，

∴∠ABD=∠BDC．

∴∠1=∠2．

∴BH//DG．

　　　　　　　　

（2）在矩形ABCD中，

∴∠A=∠C，AB=CD．

由折叠可知：AB=BE，CD=DF，∠3=∠A，∠4=∠C．

∴BE=DF，∠3=∠4．

在△BEH和△DFG中，

∴△BEH≌△DFG．

（3）①∵四边形ABCD是矩形，AB＝6cm，BC＝8cm，

∴AB＝CD＝6cm，AD＝BC＝8cm，

∴BD＝

∵由（2）知，FD＝CD，CG＝FG，

∴BF＝106＝4cm，

故答案为：4；

②设CG=x cm，则FG=x cm，BG=（8－x）cm，

在Rt△BGF中，BG2＝BF2＋FG2，

即

解得x=3

即CG=3 cm．