题目内容
【题目】如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4 ![]() ,则S阴影=( )
,则S阴影=( ) 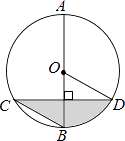
A.2π??
B.![]() π??
π??
C.![]() π??
π??
D.![]() π
π
【答案】B
【解析】解:如图,假设线段CD、AB交于点E, 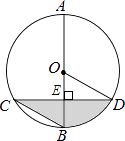
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=ED=2 ![]() ,
,
又∵∠BCD=30°,
∴∠DOE=2∠BCD=60°,∠ODE=30°,
∴OE=DEcot60°=2 ![]() ×
× ![]() =2,OD=2OE=4,
=2,OD=2OE=4,
∴S阴影=S扇形ODB﹣S△DOE+S△BEC= ![]() ﹣
﹣ ![]() OE×DE+
OE×DE+ ![]() BECE=
BECE= ![]() ﹣2
﹣2 ![]() +2
+2 ![]() =
= ![]() .
.
故选B.
【考点精析】本题主要考查了垂径定理和圆周角定理的相关知识点,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.

练习册系列答案
相关题目
【题目】下表记录了一名球员在罚球线上投篮的结果,
投篮次数(n) | 50 | 100 | 150 | 209 | 250 | 300 | 350 |
投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 175 |
投中频率(n/m) | 0.56 | 0.60 |
| 0.49 |
|
|
(1)计算并填写表中的投中频率(精确到0.01);
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?