Question

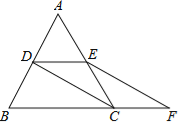
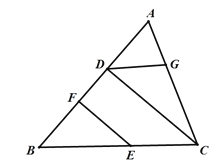
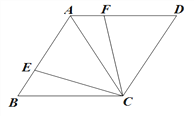
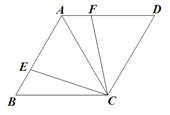
【题目】如图，四边形ABCD中，∠B=60°，对角线AC=BC，点E在AB上，将CE绕点C顺时针旋转60得CF,且点F在AD上.

（1）求证：AF=BE；

（2）若AE=DF,求证：四边形ABCD是菱形.

Answer 1

【答案】见解析

【解析】(1)、利用题意得出△ABC是等边三角形，根据等边三角形和旋转图形的性质得出∠ECF=60，然后证明△BCE和△ACF全等，从而得出答案；(2)、利用根据∠FAC=∠ACB=60得出AF∥BC，根据全等得出AD=AB，结合已知条件得出答案．

(1)、证明：∵AC=BC,∠B=60°，∴△ABC是等边三角形，

∴AB=BC=AC，∠ACB=60°，∵∠ECF=60，∴∠ACB=∠ECF，∴∠ECB=∠ACF，

在△BCE和△ACF中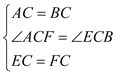，，∴△BCE≌△ACF（SAS；

∴AF=BE，∠FAC=∠B=60，

(2)、∵∠FAC=∠ACB=60 ， ∴AF∥BC，∵AF=BE, AE=DF，∴AD=AB， ∵AD=BC，

∴四边形ABCD是平行四边形， ∵AB=BC， ∴□ABCD是菱形.