题目内容
【题目】如图所示,在平面直角坐标系中,A点坐标为(-2,2).
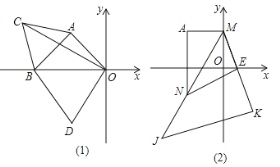
⑴如图⑴,在△ABO为等腰直角三角形,求B点坐标.
⑵如图⑴,在⑴的条件下,分别以AB和OB为边作等边△ABC和等边△OBD,连结OC,求∠COB的度数.
⑶如图⑵,过点A作AM⊥y轴于点M,点E为x轴正半轴上一点,K为ME延长线上一点,以MK为直角边作等腰直角三角形MKJ,∠MKJ=90°,过点A作AN⊥x轴交MJ于点N,连结EN.则①![]() 的值不变;②
的值不变;②![]() 的值不变,其中有且只有一个结论正确,请判断出正确的结论,并加以证明和求出其值.
的值不变,其中有且只有一个结论正确,请判断出正确的结论,并加以证明和求出其值.
【答案】(1)B(4,0);(2)30°;(3)![]() =1;
=1;
【解析】
(1)作AE⊥OB于点E,由点A的坐标就可以求出OE的值,就可以求出OB的值而得出结论.
(2)由等腰直角三角形和等边三角形的性质就可以得出∠CAO的值,再由等腰三角形的性质就可以求出∠AOC的值,从而得出结论;
(3)在AN上取一点P,使AP=OE,证明△APM≌△OEM,就可以得出MP=ME,∠AMP=∠OME,由等腰直角三角形的性质就可以得出∠PMN=∠EMN,得出△PMN≌△EMN就可以得出结论.
(1)如图1,作AE⊥OB于点E,
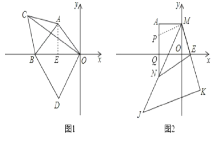
∴∠AEO=90°.
∵A(2,2).
∴OE=AE=2.
∵AB=AO,
∴BO=2EO=4.
∴B(4,0);
(2)∵△ABO为等腰直角三角形,
∴AB=AO,∠BAO=90°,∠AOB=45°.
∵△ABC是等边三角形,
∴∠BAC=60°,AC=AB,
∴∠CAO=150°,AC=AO,
∴∠ACO=∠AOC=15°,
∴∠COB=45°15°=30°;
(3) ![]() 的值不变
的值不变
理由:如图2,在AN上取一点P,使AP=OE,
∵AM⊥y轴,AN⊥x轴,
∴∠AQO=∠AMO=90°.
∵∠MOQ=90°,
∴四边形AMOQ是矩形。
∵A(2,2),
∴AQ=OQ=2,
∴四边形AMOQ是正方形,
∴∠A=∠MOE=∠AMO=90°,
AM=OM.
在△APM和△OEM中,
 ,
,
∴△APM≌△OEM(SAS),
∴MP=ME,∠AMP=∠OME.
∵∠AMP+∠PMO=90°,
∴∠OME+∠PMO=90°,
即∠PME=90°.
∵△MKJ等腰直角三角形,
∴∠JMK=45°,
∴∠PMN=45°,
∴∠PMN=∠EMN.
在△PMN和△EMN中,
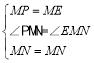 ,
,
∴△PMN≌△EMN(SAS),
∴PN=EN.
∵PN=ANAP,
∴PN=AN0E,
∴ANOE=EN.
∴![]() =1
=1