题目内容

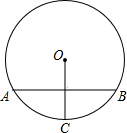
已知⊙O的半径为6cm，点P为⊙O内一点，PO=3cm，那么过点P最短的弦长是（　　）
A．
34
cm		B．3
3
cm		C．8cmD．6
3
cm
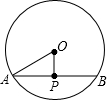
当过P的弦与OP垂直时，此时的弦长最短，连接OA，
利用垂径定理得到P为AB的中点，即AP=
1
2
AB，
在Rt△AOP中，OA=6cm，OP=3cm，
根据勾股定理得：AP=
OA2-OP2
=3
3
cm，
则过点P最短的弦长AB=6
3
cm．
故选D．
练习册系列答案
相关题目
某公园草坪的防护栏是由100段形状相同的抛物线组成的．为了牢固起见，每段护栏需要间距0.4m加设一根不锈钢的支柱，防护栏的最高点距底部0.5m（如图），则这条防护栏的不锈钢支柱AB的长度为（　　）
A．
12
25
m		B．
21
50
m		C．
3
8
m		D．
8
25
m
在半径等于5cm的圆内有长为5
3
cm的弦，则此弦所对的圆周角为（　　）
A．120°B．30°或120°C．60°D．60°或120°
⊙O的半径为10cm，两平行弦AC，BD的长分别为12cm，16cm，则两弦间的距离是（　　）
A．2cmB．14cmC．6cm或8cmD．2cm或14cm
如图，点A、B、P在以1为半径的⊙0上，点P为动点，AB=
3
，若△ABP是等腰三角形，则所有符合条件的点P有（　　）
A．1个B．2个C．3个D．4个
如图，点A，B是⊙O上两点，AB=10，点P是⊙O上的动点（P与A，B不重合）连接AP，PB，过点O分别作OE⊥AP于点E，OF⊥PB于点F，则下列结论正确的是（　　）
A．EF=2.5B．EF=
10
3
C．EF=5D．EF的长度无法确定
如图，⊙O的弦AB垂直平分半径OC，若AB=
6
，则⊙O的半径为（　　）
A．
2
B．2
2
C．
2
2
D．
6
2
圆的半径是10，弦心距为8的弦长是______．
已知：如图，在△ABC中，AB为⊙O的直径，BC，AC分别交⊙O于D、E两点，
BD
=
DE
，连接AD，求证：△ABD≌△ACD．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网