Question

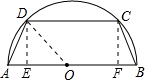
如图，有一块半径为5cm的半圆形钢板，计划截成等腰梯形ABCD的形状，他的下底AB是⊙O的直径，上底CD的端点在圆周上．
（1）若等腰梯形ABCD的高为4cm时，求梯形的上底DC的长；
（2）写出这个等腰梯形周长y（cm）和腰长x（cm）间的函数关系式，并写出x的取值范围；
（3）若腰长x（cm）限定为2≤x≤6时，分别求出等腰梯形ABCD周长的最大、最小值．

Answer 1

（1）过点D作DE⊥AB，CF⊥AB，连接OD，
∴ED=4cm，OD=5cm，
∴OE=

52-42

=3cm，
同理可求OF=3cm，
∴EF=6cm，
∵四边形DEFC为矩形，
∴DC=EF=6cm；

（2）如图，作DE⊥AB于E，连接BD．
∵AB为直径，
∴∠ADB=90°，
在Rt△ADB与Rt△AED中，∠ADB=90°=∠AED，∠BAD=∠DAE，
∴Rt△ADB∽Rt△AED，
∴

AD

AB

=

AE

AD

，即 AE=

AD2

AB

．
又AD=x，AB=10，
∴AE=

x2

10

cm，
∴CD=AB-2AE=10-2×

x2

10

=（10-

x2

5

）cm，
∴y=AB+BC+CD+AD=10+x+10-

x2

5

+x=-

1

5

x2+2x+20，
由于AD＞0，AE＞0，CD＞0，所以x＞0，

x2

5

＞0，10-

x2

5

＞0，
解得：0＜x＜5

2

；

（3）∵y=-

1

5

x2+2x+20=-

1

5

（x-5）²+25，
又∵2≤x≤6，
∴当x=5时，y有最大值25cm；
当x=2时，y有最小值23.2cm．