题目内容
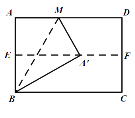
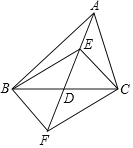
【题目】在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF≌△CDE;
(2)若AB=AC,试判断四边形BFCE是怎样的四边形,并证明你的结论.
【答案】(1)证明见解析;(2)四边形BFCE是菱形,证明见解析.
【解析】
(1)由平行线的性质得出∠ECD=∠FBD,∠DEC=∠DFB,然后再加上由中点得出的BD=DC,即可利用AAS证明△BDF≌△EDC;
(2)先根据等腰三角形的三线合一证明AD⊥BC,然后由(1)中的可得出DE=DF,DB=DC,最后利用对角线互相平分且互相垂直的四边形为菱形即可证明四边形BFCE是菱形.
(1)∵CE∥BF,
∴∠ECD=∠FBD,∠DEC=∠DFB;
又∵D是BC的中点,
∴BD=DC,
∴△BDF≌△EDC(AAS);
(2)四边形BFCE是菱形.证明如下:
∵AB=AC,
∴△ABC是等腰三角形;
又∵BD=DC,
∴AD⊥BC,
由(1)知:△BDF≌△EDC,
则DE=DF,DB=DC;
∴四边形BFCE是菱形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目