题目内容
【题目】数学问题：如何计算平面直角坐标系中任意两点之间的距离？
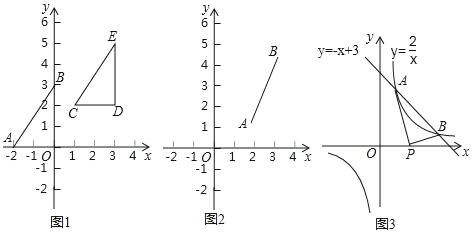
探究问题：
为解决上面的问题，我们从最简单的问题进行研究．
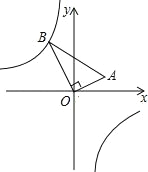
探究一：在图1中，已知线段AB，A（﹣2，0），B（0，3），写出线段AO的长，BO的长，所以线段AB的长为多少；把Rt△AOB向右平移3个单位，再向上平移2个单位，得到Rt△CDE，写出Rt△CDE的顶点坐标C，D，E，此时线段CD的长为多少，DE的长为多少，所以线段CE的长为多少．
探究二：在图2中，已知线段AB的端点坐标为A（a，b），B（c，d），求出图中AB的长（用含a，b，c，d的代数式表示，不必证明）．
归纳总结：无论线段AB处于直角坐标系中的哪个位置，当其端点坐标为A（x1，y1），B（x2，y2）时线段AB的长为多少（用含x1，y1，x2，y2的代数式表示，不必证明）．
拓展与应用：
运用在图3中，一次函数y=﹣x+3与反比例函数y=
的图象交点为A、B，交点的坐标分别是A（1，2），B（2，1）．
①求线段AB的长；
②若点P是x轴上动点，求PA+PB的最小值．
练习册系列答案
相关题目
