题目内容
【题目】（1）解不等式组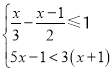
，并求出所有整数解的和．
（2）分解因式：
（3）解方程：
．
（4）先化简，再求值：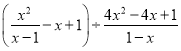
，其中
．
【答案】（1）
；
；（2）
；（3）无解；（4）
；
【解析】
（1）分别求出不等式组中两不等式的解集，得到不等式组的解集，进而求出整数解的和即可；
（2）先计算完全平方式，然后合并同类项，再进行因式分解即可；
（3）先去分母，去括号，然后移项，合并同类项，系数化为1，即可得到答案；
（4）先把分式进行化简，然后把x的值代入计算，即可得到答案.
解：（1）解不等式组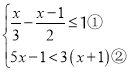
，
解不等式①，得：
，
解不等式②，得：
，
∴不等式组的解集是：，
∴不等式组的整数解为：
，
，
，0，1；
∴所有整数解的和为：
；
（2）
=
=
=
=；
（3）
，
∴
，
∴
∴
，
∴
；
检验，把代入分母，则
，
∴原分式方程无解；
（4）
=
=
=；
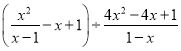
当
时，
原式=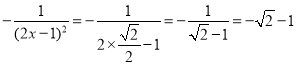
；
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
