Question

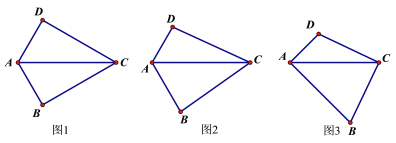
【题目】把一副三角板按如图甲放置，其中∠ACB＝∠DEC＝90°，∠A＝45°，∠D＝30°，斜边AB＝6cm，DC＝7cm．把三角板DCE绕点C顺时针旋转15°得到△D1CE1（如图乙）．这时AB与CD1相交于点O、与D1E1相交于点F．

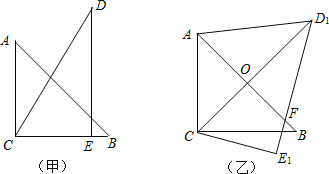
（1）求∠OFE1的度数；

（2）求线段AD1的长；

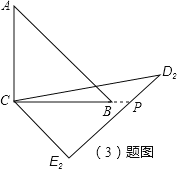
（3）若把△DCE绕着点C顺时针再旋转30°得△D2CE2，这时点B在△D2CE2的内部、外部、还是边上？说明理由．

Answer 1

【答案】（1）∠OFE1＝120°；（2）AD1＝5；（3）点B在△D2CE2的内部．理由见解析.

【解析】

（1）根据旋转角求出∠OCB＝45°，从而求出∠COB＝90°，再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解；

（2）根据等腰直角三角形的性质求出AO＝CO＝AB，再求出OD1，然后利用勾股定理列式计算即可得解；

（3）设直线CB与D2E2相交于P，然后判断出△CPE2是等腰直角三角形，再求出CP，然后与CB相比较即可得解．

（1）∵旋转角为15°，

∴∠OCB＝60°﹣15°＝45°，

∴∠COB＝180°﹣45°﹣45°＝90°，

∴CD1⊥AB，

在Rt△D1OF中，∠OFE1＝∠CD1E1+∠D1OF＝30°+90°＝120°；

（2）∵CD1⊥AB，

∴AO＝CO＝AB＝×6＝3，

∴OD1＝D1C﹣CO＝7﹣3＝4，

在Rt△AD1O中，由勾股定理得，AD1＝＝＝5；

（3）点B在△D2CE2的内部．

理由：设直线CB与D2E2相交于P，

∵△DCE绕着点C顺时针再旋转30°，

∴∠PCE2＝15°+30°＝45°，

∴△CPE2是等腰直角三角形，

∴CP＝CE2＝，

∵AB＝6，

∴CB＝AB＝3＜，即CB＜CP，

∴点B在△D2CE2的内部．