题目内容
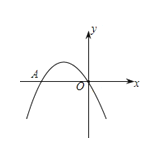
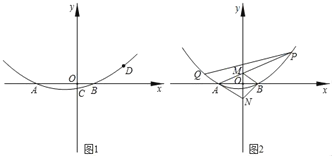
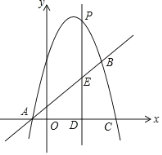
【题目】如图,已知抛物线![]() 经过点
经过点![]() 、
、![]() .
.
(1)求抛物线的解析式,并写出顶点![]() 的坐标;
的坐标;
(2)若点![]() 在抛物线上,且点
在抛物线上,且点![]() 的横坐标为8,求四边形
的横坐标为8,求四边形![]() 的面积
的面积
(3)定点![]() 在
在![]() 轴上,若将抛物线的图象向左平移2各单位,再向上平移3个单位得到一条新的抛物线,点
轴上,若将抛物线的图象向左平移2各单位,再向上平移3个单位得到一条新的抛物线,点![]() 在新的抛物线上运动,求定点
在新的抛物线上运动,求定点![]() 与动点
与动点![]() 之间距离的最小值
之间距离的最小值![]() (用含
(用含![]() 的代数式表示)
的代数式表示)
【答案】(1)![]() ,
,![]() ;(2)36;(3)
;(2)36;(3)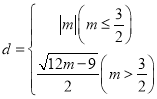
【解析】
(1)函数的表达式为:y=![]() (x+1)(x-5),即可求解;
(x+1)(x-5),即可求解;
(2)S四边形AMBC=![]() AB(yC-yD),即可求解;
AB(yC-yD),即可求解;
(3)抛物线的表达式为:y=![]() x2,即可求解.
x2,即可求解.
(1)函数的表达式为:y=![]() (x+1)(x-5)=
(x+1)(x-5)=![]() (x2-4x-5)=
(x2-4x-5)=![]() ,
,
点M坐标为(2,-3);
(2)当x=8时,y=![]() (x+1)(x-5)=9,即点C(8,9),
(x+1)(x-5)=9,即点C(8,9),
S四边形AMBC=![]() AB(yC-yD)=
AB(yC-yD)=![]() ×6×(9+3)=36;
×6×(9+3)=36;
(3)y=![]() (x+1)(x-5)=
(x+1)(x-5)=![]() (x2-4x-5)=
(x2-4x-5)=![]() (x-2)2-3,
(x-2)2-3,
抛物线的图象向左平移2个单位,再向上平移3个单位得到一条新的抛物线,
则新抛物线表达式为:y=![]() x2,
x2,
则定点D与动点P之间距离PD=![]() ,
,
∵![]() >0,PD有最小值,当x2=3m-
>0,PD有最小值,当x2=3m-![]() 时,
时,
PD最小值d=![]() .
.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目