题目内容
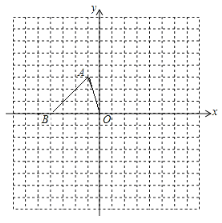
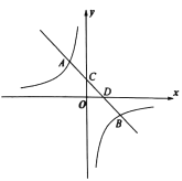
【题目】如图,一次函数![]() 的图象与双曲线
的图象与双曲线![]() 相交于A(-1,2)和B(2,b)两点,与y轴交于点C,与x轴交于点D.
相交于A(-1,2)和B(2,b)两点,与y轴交于点C,与x轴交于点D.
(1)求一次函数的解析式;
(2)根据图象直接写出不等式![]() 的解集;
的解集;
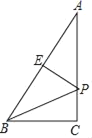
(3)经研究发现:在y轴负半轴上存在若干个点P,使得![]() 为等腰三角形。请直接写出P点所有可能的坐标.
为等腰三角形。请直接写出P点所有可能的坐标.
【答案】(1)y1=-x+1;(2)-1≤x<0或x≥2;(3)(0,-1),(0,1-![]() ),(0,-3).
),(0,-3).
【解析】
(1)将A,B坐标代入反比例函数解析式求出k,b的值,再将A,B点代入一次函数解析式可求解;
(2)由A与B交点横坐标,根据函数图象确定出所求不等式的解集即可;
(3)根据等腰三角形的性质分PC=PB,PC=BC,PB=BC求解即可.
解:(1)∵A(-1,2)和B(2,b)在双曲线![]() (k≠0)上,
(k≠0)上,
∴k=-1×2=2b,
解得b=-1.
∴B(2,-1).
∵A(-1,2)和B(2,-1)在直线y1=mx+n(m≠0)上,
∴![]() ,
,
解得![]() ,
,
∴y1=-x+1;
(2)由图象可知:-1≤x<0或x≥2是不等式![]() 的解集;
的解集;
(3)由(1)y1=-x+1可知C点的坐标为(0,1)
![]() B(2,-1)
B(2,-1)
∴BC=![]()
![]()
要使得![]() 为等腰三角形
为等腰三角形
∴PC=PB或PC=BC或PB=BC
当P1C= P1B时,设P1(0,y1),如下图

![]() B(2,-1)
B(2,-1)
则P1B=2
∴P1C= P1B=2
又![]() C(0,1),P1C=O P1+OC
C(0,1),P1C=O P1+OC
∴O P1=1,即y1=-1
P1(0,-1);
当P2C=BC时,设P2(0,y2),如下图
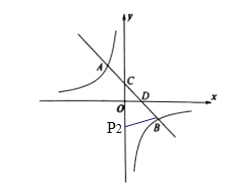
![]() BC=
BC=![]()
∴P2C=BC=![]()
又![]() C(0,1),P2C=O P2+OC
C(0,1),P2C=O P2+OC
∴O P2=![]() -1,即y2=1-
-1,即y2=1-![]()
P2(0, 1-![]() );
);
当P3B=BC时,设P3(0,y3),如下图

![]() BC=
BC=![]()
∴P3C=BC=![]()
∴CP3=![]() =4
=4
又![]() C(0,1),P3C=O P3+OC
C(0,1),P3C=O P3+OC
∴O P3=4-1=3,即y3=-3
P3(0, -3).
综上所述满足要求的P点坐标为:(0,-1),(0,1-![]() ),(0,-3).
),(0,-3).