Question

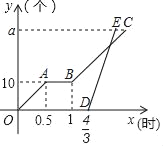
【题目】甲、乙两名工人分别加工a个同种零件．甲先加工一段时间，由于机器故障进行维修后继续按原来的工作效率进行加工，当甲加工小时后．乙开始加工，乙的工作效率是甲的工作效率的3倍．下图分别表示甲、乙加工零件的数量y（个）与甲工作时间x（时）的函数图象．解读信息：

（1）甲的工作效率为　　个/时，维修机器用了　　小时

（2）乙的工作效率是　　个/时；问题解决：

①乙加工多长时间与甲加工的零件数量相同，并求此时乙加工零件的个数；

②若乙比甲早10分钟完成任务，求a的值．

Answer 1

【答案】（1）20，0.5；（2）60；（3）①乙加工小时与甲加工零件数量相同，此时乙加工25个零件；②a=30

【解析】

(1)、根据图象可以的到甲0.5小时加工了10个零件，则可以求得甲的效率，根据图象可以直接求出甲维修机器所用时间；(2)、根据乙的效率是甲的3倍即可求得乙的效率；①、利用待定系数法求得乙的函数解析式以及甲在大于1小时时的函数解析式，求两个函数的交点；②、设乙加工零件m 个，则点E（x1，a），点C（x2，a），分别代入两个函数的解析式，根据x2-x1=小时，即可列方程组求解．

（1）甲的工作效率是10÷0.5=20（个/时），维修机器用的时间为：1﹣0.5=0.5（小时）．

（2）∵乙的工作效率是甲的工作效率的3倍，甲的工作效率是20个/时，

∴乙的工作效率是20×3=60（个/时）．

（3）①设直线BC对应的函数关系式为y=20x+b1，把点B（1，10）代入得b1=﹣10．

则直线BC所对应函数关系式为y=20x﹣10 ①．设直线DE的关系式为y=60x+b2，

把点D（，0）代入得b2=﹣80．则直线DE对应的函数关系式为y=60x﹣80②．﹣

联立①②，得：，解得：，所以交点坐标为（1.75，25）．

1.75﹣1.75﹣=（小时）．

所以乙加工小时与甲加工零件数量相同，此时乙加工25个零件；

②设点E（x1，a），点C（x2，a），分别代入y=60x﹣80，y=20x﹣10，

得x1=，x2=，∵x2﹣x1==，∴﹣=，解得：a=30．