Question

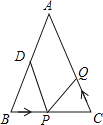
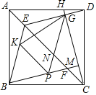
【题目】如图，四边形为正方形，是上任意一点，连接，过作于，交于，过作交于，交于，在线段上作，连接，，其中交于点，为上一点，连接，，若，，，求的值为________．

Answer 1

【答案】

【解析】

连接DF，构建菱形EBFD和平行四边形GPFD，证明KP∥EF，得△BPK∽△BFE，列比例式为=，设BP=3x，BF=5x，则PF=CM=DG=2x，EG=3x，根据BM=12列方程解出x的值，计算EG的长；设AC与KG交于点O，过K作KP⊥AC于P，过G作GQ⊥AC于Q，则KP∥GQ，根据同角的三角函数求KP、GQ、OP、OQ的长，证明△KIO∽△GQO，根据相似比为2：3分别求OK、OG的长，并相加即可得KG的长，最后计算比值即可．

连接DF，

∵四边形ABCD为正方形，

∴BC=CD，∠BCD=90°，

∴∠BCM+∠MCD=90°，

∵BM⊥CH

∴∠BMC=90°，

∴∠BCM+∠MBC=90°，

∴∠MCD=∠MBC，

∵DE∥BM，

∴∠DGC=∠BMG=90°，

∴∠DGC=∠BMC=90°，

∴△BMC≌△CGD，

∴BM=CG=12，CM=DG，

∵PF=DG，

∴PF=DG=CM，

在△ABE和△ADE中，

，

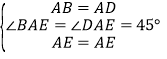∴△ABE≌△ADE（SAS），

∴BE=ED，∠AEB=∠AED，

∴∠BEF=∠FED，

∵DE∥BM，

∴∠DEF=∠EFB，

∴∠BEF=∠EFB，

∴BE=BF，

∴BE=BF=ED，

∴四边形EBFD是菱形，

∴∠BFE=∠EFD，

∴GD=PF，GD∥PF，

∴四边形GPFD是平行四边形，

∴GP∥DF，

∴∠BPG=∠BFD，

∵∠BPK=∠KPG，

∴2∠BPK=2∠BFE，

∴∠BPK=∠BFE，

∴PK∥EF，

∴△BPK∽△BFE，

∴=，

设BP=3x，BF=5x，则PF=CM=DG=2x，EG=3x，

∵FM∥DE，

∴△CFM∽△CEG，

∴，

∴，

∴FM=，

∵BM=12，

∴BF+FM=12，

5x+=12，

解得：x1=2，x2=-12（舍），

∴EG=3x=6；FM==2，CM=2x=4，

∵∠BKP=∠BPK，

∴BK=BP=3x=6，

∵BF=5x=10，

∴EK=10-6=4，

设AC与KG交于点O，过K作KI⊥AC于I，过G作GQ⊥AC于Q，则KI∥GQ，

∵∠BEF=∠DEF，

∴，

∵∠BEF=∠BFE=∠CFM，

∴tan∠BEF=tan∠CFM===2，

∵EK=4，

∴KI=，EI=，

同理得：GQ=，EQ=，

∴IQ=EQ-EI=-=，

∵KI∥GQ，

∴△KIO∽△GQO，

∴，

∴，

∴OI=×IQ=×=，

由勾股定理得：OK===，

∴OG=，

∴KG=OK+OG=，

∴ ==，

故答案为：.