题目内容

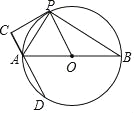
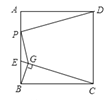
【题目】如图，已知正方形ABCD的边长是4，点E是AB边上一动点，连接CE，过点B作BG⊥CE于点G，点P是AB边上另一动点，则PD+PG的最小值是（ ）

A. B. C. D.

【答案】C

【解析】

作DC关于AB的对称点D′C′，以BC中的O为圆心作半圆O，连D′O分别交AB及半圆O于P、G．将PD+PG转化为D′G找到最小值．

解：如图：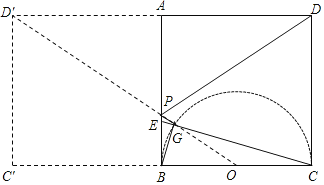

取点D关于直线AB的对称点D′．以BC中点O为圆心，OB为半径画半圆．
连接OD′交AB于点P，交半圆O于点G，连BG．连CG并延长交AB于点E．
由以上作图可知，BG⊥EC于G．
PD+PG=PD′+PG=D′G
由两点之间线段最短可知，当点D′，G，O三点共线时，PD+PG最小．
∵D′C′=4，OC′=6
∴D′O=
∴D′G=22
∴PD+PG的最小值为22
故选C.

练习册系列答案
相关题目

【题目】为了解某校九年级男生的体能情况，体育老师从中随机抽取部分男生进行引体向上测试，并对成绩进行了统计，绘制成尚不完整的扇形图和条形图，根据图形信息回答下列问题：

（1）本次抽测的男生有________人，抽测成绩的众数是_________；

（2）请将条形图补充完整；

（3）若规定引体向上6次以上（含6次）为体能达标，则该校125名九年级男生中估计有多少人体能达标？

【题目】如图是二次函数(a，b，c是常数，a≠0)图象的一部分，与x轴的交点A在点(2 ，0)和(3 ，0)之间，对称轴是x=1．对于下列结论：① ab＜0；② 2a+b=0；③ 3a+c＞0；④a+b≥m(am+b)(m为实数)；⑤ 当－1＜x＜3时，y＞0. 其中正确结论的个数为( )

A. 2个B. 3个C. 4个D. 5个

【题目】如图,将两张长为5,宽为1的矩形纸条交叉,让两个矩形对角线交点重合,且使重叠部分成为一个菱形.当两张纸条垂直时,菱形周长的最小值是4,把一个矩形绕两个矩形重合的对角线交点旋转一定角度,在旋转过程中,得出所有重叠部分为菱形的四边形中,周长的最大值是(　　)

A. 8B. 10C. 10.4D. 12

【题目】如图，已知AB是⊙O的直径，PC切⊙O于点P，过A作直线AC⊥PC交⊙O于另一点D，连接PA、PB．

(1)求证：AP平分∠CAB；

(2)若P是直径AB上方半圆弧上一动点，⊙O的半径为2，则

①当弦AP的长是_____时，以A，O，P，C为顶点的四边形是正方形；

②当的长度是______时，以A，D，O，P为顶点的四边形是菱形．

【题目】如图，⊙O是△ABC的外接圆，AC是直径，弦BD＝BA，EB⊥DC，交DC的延长线于点E．

（1）求证：BE是⊙O的切线；

（2）当sin∠BCE＝，AB＝3时，求AD的长．

【题目】如图， 是⊙的直径，点是⊙上一点， 与过点的切线垂直，垂足为点，直线与的延长线相交于点，弦平分∠，交于点，连接．

（1）求证： 平分∠；

（2）求证：PC=PF；

（3）若，AB=14，求线段的长．

【题目】如图，在Rt△ABC中，∠C=90°，BE平分∠ABC交AC于点E，作ED⊥EB交AB于点D，⊙O是△BED的外接圆．

（1）求证：AC是⊙O的切线；

（2）已知⊙O的半径为2.5，BE=4，求BC，AD的长．

【题目】在中，、是边上的三等分点，是边上的中线，、分为三段的长分别是、、，若这三段有，则等于( )

A. B. C. D.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网