题目内容
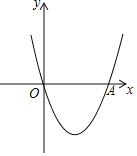
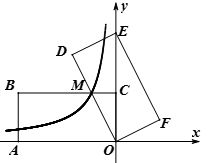
【题目】如图,将两张长为5,宽为1的矩形纸条交叉,让两个矩形对角线交点重合,且使重叠部分成为一个菱形.当两张纸条垂直时,菱形周长的最小值是4,把一个矩形绕两个矩形重合的对角线交点旋转一定角度,在旋转过程中,得出所有重叠部分为菱形的四边形中,周长的最大值是( )
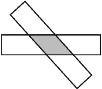
A. 8B. 10C. 10.4D. 12
【答案】C
【解析】
作出图形，确定当两矩形纸条有一条对角线互相重合时，菱形的周长最大，设菱形的边长为x，表示出AB，然后利用勾股定理列式进行计算求出x，再根据菱形的四条边都相等解答．
如图，菱形的周长最大，
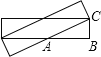
设菱形的边长AC=x，则AB=5-x，
在Rt△ABC中，AC2=AB2+BC2，
即x2=（5-x）2+12，
解得x=2.6，
所以，菱形的最大周长=2.6×4=10.4．
故选C．
【题目】已知y是x的函数，自变量x的取值范围是x＞0，下表是y与x的几组对应值．
x | … | 1 | 2 | 4 | 5 | 6 | 8 | 9 | … |
y | … | 3.92 | 1.95 | 0.98 | 0.78 | 2.44 | 2.44 | 0.78 | … |
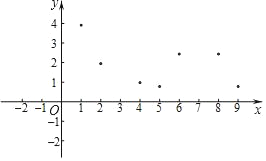
小风根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象和性质进行了探究．
下面是小风的探究过程，请补充完整：
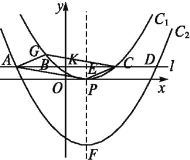
（1）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（2）根据画出的函数图象，写出：
①x＝7对应的函数值y约为多少；
②写出该函数的一条性质．
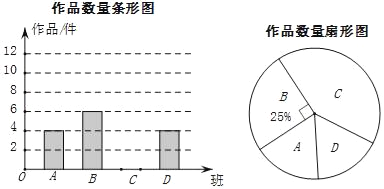
【题目】为了了解学生关注热点新闻的情况，“两会”期间，小明对班级同学一周内收看“两会”新闻的次数情况作了调查，调查结果统计如图所示（其中男生收看
次的人数没有标出）.
根据上述信息，解答下列各题：
×
（1）该班级女生人数是__________，女生收看“两会”新闻次数的中位数是________；
（2）对于某个群体，我们把一周内收看某热点新闻次数不低于次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低
，试求该班级男生人数；
（3）为进一步分析该班级男、女生收看“两会”新闻次数的特点，小明给出了男生的部分统计量（如表）.
统计量 | 平均数（次） | 中位数（次） | 众数（次） | 方差 | … |
该班级男生 |
|
|
|
| … |
根据你所学过的统计知识，适当计算女生的有关统计量，进而比较该班级男、女生收看“两会”新闻次数的波动大小.
