题目内容
【题目】在![]() 中,
中,![]() 、
、![]() 是
是![]() 边上的三等分点,
边上的三等分点,![]() 是
是![]() 边上的中线,
边上的中线,![]() 、
、![]() 分
分![]() 为三段的长分别是
为三段的长分别是![]() 、
、![]() 、
、![]() ,若这三段有
,若这三段有![]() ,则
,则![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
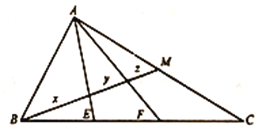
设BM分别交AE,AF于P,Q,连接MF, 作FH//BM交AC于H,根据中点的性质可得EP//MF,根据BE=EF,得到BP=PM,根据平行线分线段成比例定理可得CF:CB=FH:BM=CH:CM=1:3,则FH:QM=AH:AM=5:3, 设FH=t,所以BM=3t,QM=0.6t,BP=1.5t,
PQ=0.9t,即可求解.
设BM分别交AE,AF于P,Q,连接MF,
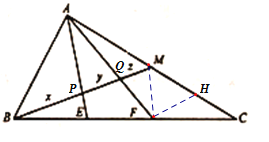
因为MF//AE,所以EP//MF,又因为BE=EF,所以BP=PM
作FH//BM交AC于H,CF:CB=FH:BM=CH:CM=1:3,
![]() FH:QM=AH:AM=5:3,
FH:QM=AH:AM=5:3,
设FH=t,所以BM=3t,QM=0.6t,BP=1.5t,PQ=0.9t
所以BP:PQ:QM=5:3:2
即x:y:z=5:3:2
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目