题目内容
【题目】如图, ![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 是⊙
是⊙![]() 上一点,
上一点, ![]() 与过点
与过点![]() 的切线垂直,垂足为点
的切线垂直,垂足为点![]() ,直线
,直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,弦
,弦![]() 平分∠
平分∠![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
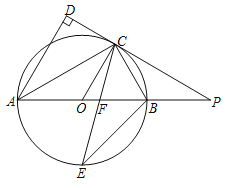
(1)求证: ![]() 平分∠
平分∠![]() ;
;
(2)求证:PC=PF;
(3)若![]() ,AB=14,求线段
,AB=14,求线段![]() 的长.
的长.
【答案】(1)证明过程见解析;(2)证明过程见解析;(2)24.
【解析】试题分析:(1)根据切线以及AD⊥PD得出OC∥AD,得到∠ACO=∠DAC,然后根据OC=OA得出∠ACO=∠CAO,从而得到∠DAC=∠CAO,即角平分线;(2)根据题意得出∠PFC=∠PCF,得出PC=PF;(3)根据题意得出△PAC∽△PCB,根据tan∠ABC可得![]() ,设PC=4k,PB=3k,根据Rt△POC得出PO=3k+7,根据AB的长度得出OC的长度,根据
,设PC=4k,PB=3k,根据Rt△POC得出PO=3k+7,根据AB的长度得出OC的长度,根据![]() 得出k的值,然后求出PC的长度.
得出k的值,然后求出PC的长度.
试题解析:(1)∵PD切⊙O于点C,∴OC⊥PD
又AD⊥PD,∴OC∥AD.∴∠ACO=∠DAC.
又OC=OA,∴∠ACO=∠CAO,
∴∠DAC=∠CAO,即AC平分∠DAB.
(2)∵AD⊥PD,∴∠DAC+∠ACD=90°.
又AB为⊙O的直径,∴∠ACB=90°.
∴∠PCB+∠ACD=90°,
∴∠DAC=∠PCB.
又∠DAC=∠CAO,∴∠CAO=∠PCB.
∵CE平分∠ACB,∴∠ACF=∠BCF,
∴∠CAO+∠ACF=∠PCB+∠BCF,
∴∠PFC=∠PCF,
∴PC=PF
(3)∵∠PAC=∠PCB,∠P=∠P,
∴△PAC∽△PCB,
∴![]() .
.
又tan∠ABC=![]() ,
,
∴![]() ,
,
∴![]()
设![]() ,
, ![]() ,则在Rt△POC中,
,则在Rt△POC中, ![]() ,
,
∵AB=14,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴k=6 (k=0不合题意,舍去).
∴![]() .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案【题目】张老师打算在小明和小白两位同学之间选一位同学参加数学竞赛,他收集了小明、小白近期10次数学考试成绩,并绘制了折线统计图(如图所示)
项目 | 众数 | 中位数 | 平均数 | 方差 | 最高分 |
小明 | 85 | 85 | |||
小白 | 70,100 | 85 | 100 |
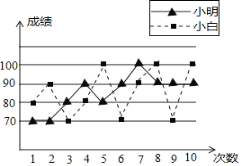
(1)根据折线统计图,张老师绘制了不完整的统计表,请你补充完整统计表;
(2)你认为张老师会选择哪位同学参加比赛?并说明你的理由