题目内容
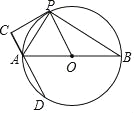
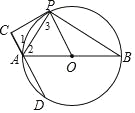
【题目】如图,已知AB是⊙O的直径,PC切⊙O于点P,过A作直线AC⊥PC交⊙O于另一点D,连接PA、PB.
(1)求证:AP平分∠CAB;
(2)若P是直径AB上方半圆弧上一动点,⊙O的半径为2,则
①当弦AP的长是_____时,以A,O,P,C为顶点的四边形是正方形;
②当![]() 的长度是______时,以A,D,O,P为顶点的四边形是菱形.
的长度是______时,以A,D,O,P为顶点的四边形是菱形.
【答案】(1)证明见解析;(2)①2![]() ;②
;②![]() π或
π或![]() π.
π.
【解析】
(1)利用切线的性质得OP⊥PC,再证明AC∥OP得到∠1=∠3,加上∠2=∠3,所以∠1=∠2;
(2)①当∠AOP=90°,根据正方形的判定方法得到四边形AOPC为正方形,从而得到AP=2![]() ;
;
②根据菱形的判定方法,当AD=AP=OP=OD时,四边形ADOP为菱形,所以△AOP和△AOD为等边三角形,然后根据弧长公式计算![]() 的长度.当AD=DP=PO=OA时,四边形ADPO为菱形,△AOD和△DOP为等边三角形,则∠AOP=120°,根据弧长公式计算
的长度.当AD=DP=PO=OA时,四边形ADPO为菱形,△AOD和△DOP为等边三角形,则∠AOP=120°,根据弧长公式计算![]() 的长度.
的长度.
(1)∵PC切⊙O于点P,
∴OP⊥PC,
∵AC⊥PC,
∴AC∥OP,
∴∠1=∠3,
∵OP=OA,
∴∠2=∠3,
∴∠1=∠2,
∴AP平分∠CAB;
(2)①当∠AOP=90°,四边形AOPC为矩形,而OA=OP,此时矩形AOPC为正方形,
AP=![]() OP=2
OP=2![]() ;
;
②当AD=AP=OP=OD时,四边形ADOP为菱形,△AOP和△AOD为等边三角形,则∠AOP=60°,![]() 的长度=
的长度=![]() =
=![]() π.
π.
当AD=DP=PO=OA时,四边形ADPO为菱形,△AOD和△DOP为等边三角形,则∠AOP=120°,![]() 的长度=
的长度=![]() .
.
故答案为2![]() ;
;![]() π或
π或![]() π.
π.

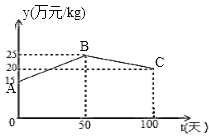
【题目】经过市场调查得知,某种商品的销售期为100天,设该商品销量单价为y(万元/kg),y与时间t(天)函数关系如下图所示,其中线段AB表示前50天销售单价y(万元/kg)与时间t(天)的函数关系;线段BC的函数关系式为y=-![]() t+m.该商品在销售期内的销量如下表:
t+m.该商品在销售期内的销量如下表:
时间t(天) | 0<t≤50 | 50<t≤100 |
销量(kg) | 200 |
|
(1)分别求出当0<t≤50和50<t≤100时y与t的函数关系式;
(2)设每天的销售收入为w(万元),则当t为何值时,w的值最大?求出最大值;