��Ŀ����
����Ŀ����֪���κ���y=x2��2x��3
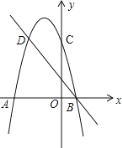
��1���������֪�Ķ��κ�������y=��x��h��2+k����ʽ������ƽ��ֱ������ϵ�л�������ͼ��
��2�����A��x1��y1����B��x2��y2���ǣ�1�������ϵ����㣬��x1��x2��1����ֱ��д��y1��y2�Ĵ�С��ϵΪ�� ����
��3�����ã�1���е�ͼ���ʾ������x2��2x��1=0�ĸ������ڣ�1����ͼ���ϼ��ɣ�Ҫ������ͼ�ۼ���

���𰸡���1����ͼ����������2��y1��y2����3����ͼ��x1��x2Ϊ����x2��2x��1=0��������
��������
��1���Ȱѽ���ʽ��ɶ���ʽ�õ������ߵĶ�������Ϊ��1��-4�����������������y��Ľ����������������x��Ľ������꣬Ȼ��������㷨�������κ���ͼ����
��2�����ö��κ��������ʽ�����⣻
��3����ֱ��y=-2�������ߵĽ��㣬��������ĺ�����Ϊ����x2-2x-1=0��������
��1��y=x2��2x��3=��x��1��2��4��
�����ߵĶ�������Ϊ��1����4����
��x=0ʱ��y=x2��2x��3=��3������������y��Ľ�������Ϊ��0����3����
��y=0ʱ��x2��2x��3=0�����x1=��1��x2=3����������x��Ľ�������Ϊ����1��0������3��0����
��ͼ��

��2�������ߵĶԳ���Ϊֱ��x=1��
��x1��x2��1����
��y1��y2��
�ʴ�Ϊy1��y2��
��3����ͼ��x1��x2Ϊ����x2��2x��1=0��������

����Ŀ���������б���Ķ�Ӧֵ��
x | 3.23 | 3.24 | 3.25 | 3.26 |
| ��0.06 | ��0.02 | 0.03 | 0.09 |
д������![]() (a��0��a��b��cΪ����)һ����x�ķ�Χ��__��
(a��0��a��b��cΪ����)һ����x�ķ�Χ��__��