题目内容
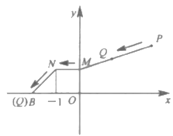
【题目】如图,已知![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,先移动到
点出发,先移动到![]() 轴上的点
轴上的点![]() 处,再沿垂直于
处,再沿垂直于![]() 轴的方向向左移动1个单位至点
轴的方向向左移动1个单位至点![]() 处,最后移动到点
处,最后移动到点![]() 处停止.当点
处停止.当点![]() 移动的路径最短时 (即三条线段
移动的路径最短时 (即三条线段![]() 、
、![]() 、
、![]() 长度之和最小),点
长度之和最小),点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
将BN向右平移1个单位得到AM,连接AB,可得四边形ABNM是平行四边形,当A,M,P在同一直线上时,AM+PM有最小值,即为线段AP的长,因此BN+PM的最小值为AP长,此时PM、MN、NB长度之和最小,通过求直线AP的解析式,即可得到点M的坐标.
解:如图,将BN向右平移1个单位得到AM,连接AB,则BN=AM,
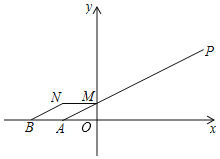
易得,四边形ABNM是平行四边形,
∴MN=AB=1,
∴当A,M,P在同一直线上时,AM+PM有最小值,最小值为线段AP的长,
因此BN+PM的最小值也为AP长,
此时PM、MN、NB长度之和最小,
∵P(3,2),B(-2,0),AB=1,
∴A(-1,0),
设直线AP的解析式为y=kx+b,将P(3,2),A(-1,0)代入得,
![]() ,
,
解得![]() ,
,
∴直线AP解析式为![]() ,
,
当x=0时,![]() ,即M点坐标为(0,
,即M点坐标为(0,![]() ),
),
故选:A.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目