题目内容
【题目】已知,如图,等腰Rt△ABC,等腰Rt△ADE,AB⊥AC,AD⊥AE,AB=AC,AD=AE,CD交AE、BE分别于点M、F.

(1)求证:△DAC≌△EAB.
(2)求证:CD⊥BE.
【答案】(1)见解析;(2)见解析
【解析】
(1)由角的和差关系可得∠DAC=∠EAB,由SAS即可得出△DAC≌△EAB;(2)由全等三角形的性质得出∠ACD=∠ABE,由对顶角∠CGF=∠AGB和三角形内角和定理得∠CFB=∠BAC=90°,即可得出结论.
(1)∵AB⊥AC,AD⊥AE,
∴∠BAC=∠DAE=90°,
∴∠DAE+∠CAE=∠BAC+∠CAE,
∴∠DAC=∠EAB,
在△DAC和△EAB中,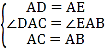
∴△DAC≌△EAB(SAS).
(2)∵△DAC≌△EAB,
∴∠ACD=∠ABE,
∵∠CGF=∠AGB,
∴由三角形内角和定理得:∠CFB=∠BAC=90°,
∴CD⊥BE.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目