题目内容
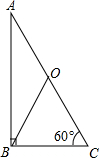 如图所示,△ABC中,∠ABC=90°,O为△ABC的外心,∠C=60°,BC=2.若△AOB面积=a,△OBC面积=b,则下列叙述何者正确
如图所示,△ABC中,∠ABC=90°,O为△ABC的外心,∠C=60°,BC=2.若△AOB面积=a,△OBC面积=b,则下列叙述何者正确
- A.a>b
- B.a<b
- C.a-b=0
- D.a+b=4
C
分析:由于直角三角形的外心是斜边的中点,即OA=OC;由此可知:△AOB和△BOC等底同高,故两者的面积相等,即a=b.
解答:∵△ABC中,∠ABC=90°,O为△ABC的外心;
∴OA=OC,
∴△AOB和△BOC等底同高,
∴S△AOB=S△BOC,即a=b,
∴a-b=0.
故选C.
点评:本题考查的知识点有两个:
①直角三角形的外心在斜边上,与斜边的中点重合;
②若两个三角形等底等高,则这两个三角形的面积相等.
分析:由于直角三角形的外心是斜边的中点,即OA=OC;由此可知:△AOB和△BOC等底同高,故两者的面积相等,即a=b.
解答:∵△ABC中,∠ABC=90°,O为△ABC的外心;
∴OA=OC,
∴△AOB和△BOC等底同高,
∴S△AOB=S△BOC,即a=b,
∴a-b=0.
故选C.
点评:本题考查的知识点有两个:
①直角三角形的外心在斜边上,与斜边的中点重合;
②若两个三角形等底等高,则这两个三角形的面积相等.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
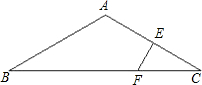 如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF. 16、如图所示,△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、AC于D、E,∠CAE:∠EAB=5:2,则∠B=
16、如图所示,△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、AC于D、E,∠CAE:∠EAB=5:2,则∠B=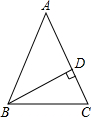 如图所示,△ABC中,AB=AC=10,BD是AC边的高线,DC=2,试求BD的长.
如图所示,△ABC中,AB=AC=10,BD是AC边的高线,DC=2,试求BD的长. 如图所示,△ABC中,BC的垂直平分线交AB于点E,若△ABC的周长为10,BC=4,则△ACE的周长是
如图所示,△ABC中,BC的垂直平分线交AB于点E,若△ABC的周长为10,BC=4,则△ACE的周长是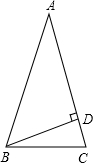 如图所示,△ABC中,AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.
如图所示,△ABC中,AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.