题目内容
【题目】中点、平行线、等腰直角三角形、等边三角形都是常见的几何图形!
(1)如图1,若点D为等腰直角三角形ABC斜边BC的中点,点E,F分别在AB、AC边上,且∠EDF=90°,连接AD、EF,当BC=5 ![]() ,FC=2时,求EF的长度;
,FC=2时,求EF的长度;
(2)如图2,若点D为等边三角形ABC边BC的中点,点E,F分别在AB,AC边上,且∠EDF=90°;M为EF的中点,连接CM,当DF∥AB时,证明:3ED=2MC;
(3)如图3,若点D为等边三角形ABC边BC的中点,点E,F分别在AB,AC边上,且∠EDF=90°;当BE=6,CF=0.8时,直接写出EF的长度.
【答案】
(1)解:如图1
∵点D为等腰直角三角形ABC斜边BC的中点
∴AD⊥BC,AD= ![]() BC=CD=
BC=CD= ![]() ,∠DAE=∠C=45°
,∠DAE=∠C=45°
∴AC= ![]() CD=5
CD=5
又∵∠EDF=90°,FC=2
∴∠ADE=∠CDF,AF=5﹣2=3
在△ADE和△CDF中
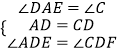
∴△ADE≌△CDF(ASA)
∴AE=CF=2
∴在Rt△AEF中,EF= ![]() =
= ![]()
(2)解:设等边三角形边长为2a,则BD=CD=a,
∵等边三角形ABC中,DF∥AB
∴∠FDC=∠B=60°
∵∠EDF=90°
∴∠BDE=30°
∴DE⊥BE
∴BE= ![]() a,DE=
a,DE= ![]() a,
a,
如图2,连接DM,

则Rt△DEF中,DM= ![]() EF=FM
EF=FM
∵∠FDC=∠FCD=60°
∴△CDF是等边三角形
∴CD=CF=a
∴CM垂直平分DF
∴∠DCN=30°
∴Rt△CDN中,DN= ![]() a,CN=
a,CN= ![]() a,DF=a
a,DF=a
∴在Rt△DEF中,EF= ![]() a=
a= ![]() a
a
∵M为EF的中点
∴FM=DM= ![]() a
a
∴Rt△MND中,MN= ![]() =
= ![]() a
a
∴CM= ![]() +
+ ![]() =
= ![]() a
a
∴ ![]() =
= ![]() =
= ![]() a
a
∴3ED=2MC;
(3)解:如图3,延长FD至G,使得FD=DG,连接EG,BG,

则ED垂直平分FG,故EF=EG
∴由BD=CD,∠BDG=∠CDF,DF=DG可得:△BDG≌△CDF
∴∠GBD=∠C=60°,BG=CF=0.8
∴∠EBG=60°+60°=120°
∴∠EBH=60°
过E作EH⊥BG于点H,则BH= ![]() BE=3
BE=3
∴Rt△BEH中,HE= ![]() =3
=3 ![]()
∴Rt△EHG中,EG= ![]() =
= ![]()
∴EF的长度为 ![]()
【解析】(1)根据已知条件点D为等腰直角三角形ABC斜边BC的中点,可求出AD、AC的长,再证明△ADE≌△CDF,就可以求出AE的长,再在Rt△AEF中,根据勾股定理可求得EF的长。
(2)设等边三角形边长为2a,则BD=CD=a,由已知条件易证得DE⊥BE,求出BE的长,连接DM,易证△CDF是等边三角形,根据CM垂直平分DF,求出CN的长,在Rt△MND中求得MN的长,然后求出CM与DN的长度之比,即可得出结论。
(3)根据题意,可添加辅助线延长FD至G,使得FD=DG,连接EG,BG,可得ED垂直平分FG,再证明△BDG≌△CDF,就可以求出BG的长和∠EBG、∠EBH的度数,由∠EBH=60°,过E作EH⊥BG于点H,然后在Rt△BEH中、Rt△EHG中就可求出EF的长。
【考点精析】掌握线段垂直平分线的性质和等腰三角形的性质是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;等腰三角形的两个底角相等(简称:等边对等角).

 阅读快车系列答案
阅读快车系列答案





