Question

【题目】已知直线AB//CD,P是两条直线之间一点，且AP⊥PC于P.

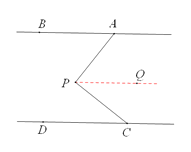
(1) 如图1,求证：∠BAP+∠DCP=90°；

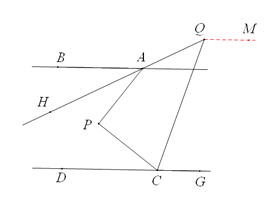
(2)如图2，CQ平分∠PCG,AH平分∠BAP,直线AH、CQ交于Q,求∠AQC的度数；

Answer 1

【答案】(1)证明见解析；(2)；

【解析】

（1）过P作PQ∥AB，由平行线的性质，得到∠BAP=∠APQ，∠DCP=∠CPQ，结合AP⊥PC，即可得到答案；

（2）过Q作QM∥AB，由平行线的性质和角平分线的性质，得到角度之间的关系，即可得到答案；

（1）证明：过P作PQ∥AB，

∴∠BAP=∠APQ

∵AB//CD

∴PQ//CD

∴∠DCP=∠CPQ

∴∠BAP+∠DCP=∠APQ+∠CPQ=∠APC

又∵AP⊥PC于P

∴∠APC=90°

∴∠BAP+∠DCP=90°；

(2) 解：过Q作QM∥AB，

∵CQ平分∠PCG ，AH平分∠BAP，

设∠PCQ=∠QCG=a ，∠BAH=∠HAP=b，

∵QM∥AB，∠BAQ=180°b

∴∠BAQ=∠AQM=180°

又∵AB//CD，

∴MQ//CD，

∴∠CQM=180°a

∴∠AQC=(180°b)(180°a)=ab

又∵由(1)得∴∠BAP+∠DCP=90°

∵∠DCP=180°2a ，∠BAP=2b

∴2b+180°2a=90°

∴ab=45°

∴∠AQC=45°；