题目内容
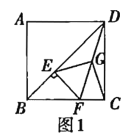
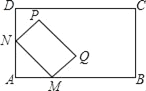
【题目】如图，四边形ABCD中，∠C＝90°，AD⊥DB，点E为AB的中点，DE∥BC.
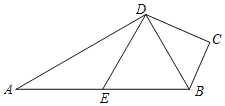
（1）求证：BD平分∠ABC；
（2）连接EC，若∠A＝30°，DC＝
，求EC的长.
【答案】（1）见解析；（2）
.
【解析】
（1）直接利用直角三角形的性质得出
，再利用DE∥BC，得出∠2＝∠3，进而得出答案；
（2）利用已知得出在Rt△BCD中，∠3＝60°，
，得出DB的长，进而得出EC的长.
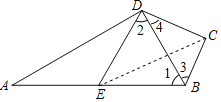
（1）证明：∵AD⊥DB，点E为AB的中点，
∴.
∴∠1＝∠2.
∵DE∥BC，
∴∠2＝∠3.
∴∠1＝∠3.
∴BD平分∠ABC.
（2）解：∵AD⊥DB，∠A＝30°，
∴∠1＝60°.
∴∠3＝∠2＝60°.
∵∠BCD＝90°，
∴∠4＝30°.
∴∠CDE＝∠2+∠4＝90°.
在Rt△BCD中，∠3＝60°，，
∴DB＝2.
∵DE＝BE，∠1＝60°，
∴DE＝DB＝2.
∴
.
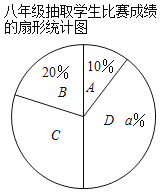
【题目】为加强学生对“垃圾分类知识”的重视程度，某学校组织了“垃圾分类知识”比赛．现七、八年级各抽取10名同学的成绩进行统计分析（成绩得分用x表示，共分成四组：A：60≤x＜70，B：70≤x＜80，C：80≤x＜90，D：90≤x≤100），绘制了如下的图表，请根据图中的信息解答下列问题：
七年级10名学生的成绩是：69，78，96，77，68，95，86，100，85，86
八年级10名学生的成绩在C组中的数据是：86，87，87
七、八年级抽取学生比赛成绩统计表
年级 | 平均数 | 中位数 | 众数 | 方差 |
七年级 | 84 | 85.5 | b | 109.6 |
八年级 | 84 | c | 92 | 102.6 |
（1）直接写出上述图表中a，b，c的值：a＝ ，b＝ ，c＝ ．
（2）根据以上数据，你认为该校七、八年级中哪个年级学生掌握垃圾分类知识较好？请说明理由（一条理由即可）： ．
（3）若两个年级共680人参加了此次比赛，估计参加此次比赛成绩优秀（90≤x≤100）的学生人数是多少？
