Question

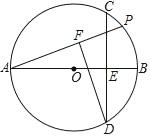
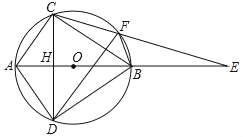
【题目】如图，AB为⊙O的直径，弦CD⊥AB于H，E为AB延长线上一点，CE交⊙O于点F

（1）求证：BF平分∠DFE；

（2）若EF＝DF，BE＝5，AH＝，求⊙O的半径．

Answer 1

【答案】（1）见解析；（2）．

【解析】

（1）根据圆内接四边形性质和圆周角定理求出∠EFB＝∠CDB，∠BCD＝∠DFB，根据垂径定理求出CH＝DH，求出BC＝BD，根据等腰三角形性质求出∠BCD＝∠CDB，求出∠EFB＝∠DFB即可；

（2）根据全等三角形的判定求出△DFB≌△EFB，根据全等三角形的性质求出BD＝BE＝5，证△DHB∽△ADB，根据相似得出比例式，代入求出即可．

（1）证明：∵C、D、B、F四点共圆，

∴∠EFB＝∠CDB，∠BCD＝∠DFB，

∵CD⊥OA，OA过O，

∴CH＝DH，

∴BC＝BD，

∴∠BCD＝∠CDB，

∴∠EFB＝∠DFB，

∴BF平分∠DFE；

（2）解：设⊙O的半径为R，

∵在△DFB和△EFB中 ,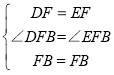

∴△DFB≌△EFB（SAS），

∴BD＝BE，

∵BE＝5，

∴BD＝5，

∵AB为⊙O直径，CD⊥AB，

∴∠ADB＝∠DHB＝90°，

∵∠DBH＝∠ABD，

∴△DHB∽△ADB，

∴，

∵AH＝，BD＝5，AB＝2R，BH＝2R﹣，

∴,

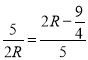解得：R＝，R＝﹣2（舍去），

即⊙O的半径是．