题目内容
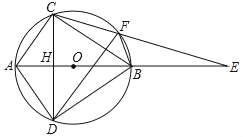
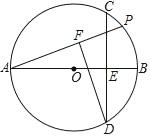
【题目】已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )
A.![]() πB.
πB.![]() C.
C.![]() πD.2
πD.2
【答案】A
【解析】
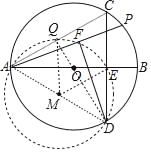
作DQ⊥AC于Q,如图,当P点在C点时,F点与Q重合;当P点在B点时,F点与E点重合,利用圆周角定理的推论判断点F在以AD为直径的圆上,则点F运动的路径为弧QE,再计算MQ的长度和∠QME的度数,然后根据弧长公式计算F运动的路径长度.
解:作DQ⊥AC于Q,如图,
当P点在C点时,F点与Q重合;当P点在B点时,F点与E点重合,
∵∠AFD=90°,
∴点F在以AD为直径的圆上,
∴点F运动的路径为弧QE,
∵弦CD⊥AB且过OB的中点,
∴OE=![]() OD,CE=DE=
OD,CE=DE=![]() ,AC=AD=2
,AC=AD=2![]() ,
,
∴∠DOE=60°,
∴∠DAC=60°,
∴△ACD为等边三角形,
∴MQ和ME为中位线,
∴MQ=![]() ,∠QME=60°,
,∠QME=60°,
∴F运动的路径长度=![]() .
.
故选A.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
【题目】某水果批发市场规定,批发苹果不少于![]() 时,批发价为5元/
时,批发价为5元/![]() .小王携带现金4000元到这市场采购苹果,并以批发价买进.
.小王携带现金4000元到这市场采购苹果,并以批发价买进.
(Ⅰ)根据题意,填表:
购买数量 |
|
|
|
|
花费 |
|
| ||
剩余现金 |
|
|
(Ⅱ)设购买的苹果为![]() ,小王付款后还剩余现金
,小王付款后还剩余现金![]() 元.求
元.求![]() 关于
关于![]() 的函数解析式,并指出自变量
的函数解析式,并指出自变量![]() 的取值范围;
的取值范围;
(Ⅲ)根据题意填空:若小王剩余现金为700元,则他购买__________![]() 的苹果.
的苹果.