题目内容
【题目】在平面直角坐标系中，先将抛物线y＝2x2﹣4x关于y轴作轴对称变换，再将所得的抛物线，绕它的顶点旋转180°，那么经两次变换后所得的新抛物线的函数表达式为（ ）
A.y＝﹣2x
﹣4xB.y＝﹣2x+4x
C.y＝﹣2x﹣4x﹣4D.y＝﹣2x+4x+4
【答案】C
【解析】
若抛物线关于y轴作轴对称变换，则图象上所有的点纵坐标不变横坐标互为相反数；将其绕顶点旋转180°后，开口大小和顶点坐标都没有变化，变化的只是开口方向，可据此得出所求的结论．
解：抛物线y＝2x2﹣4x关于y轴作轴对称变换，
所得抛物线为y＝2（﹣x）2﹣4（﹣x）＝2x2+4x；
∵y＝2x2+4x＝2（x+1）2﹣2，
∴绕顶点旋转180°后，得：y＝﹣2（x+1）2﹣2＝﹣2x2﹣4x﹣4，
故选：C．
练习册系列答案
发散思维新课堂系列答案
相关题目
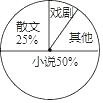
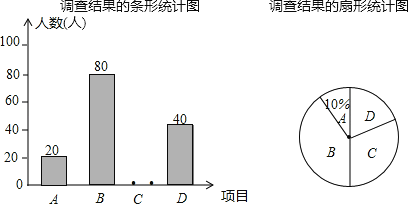
【题目】九年级一班开展了“读一本好书”的活动，班委会对学生阅读书籍的情况进行了问卷调查，问卷设置了“小说”“戏剧”“散文”“其他”四个类型，每位同学仅选一项，根据调查结果绘制了不完整的频数分布表和扇形统计图．
类别 | 频数（人数） | 频率 |
小说 | 0.5 | |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | 1 |
根据图表提供的信息，解答下列问题：
（1）九年级一班有多少名学生？
（2）请补全频数分布表，并求出扇形统计图中“其他”类所占的百分比；
（3）在调查问卷中，甲、乙、丙、丁四位同学选择了“戏剧”类，现从以上四位同学中任意选出 2 名同学参加学校的戏剧兴趣小组，请用画树状图或列表法的方法，求选取的 2 人恰好是乙和丙的概率．
