题目内容
如图1,把边长分别是为4和2的两个正方形纸片OABC和OD′E′F′叠放在一起.
(1)操作1:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转45°得到正方形ODEF,如图2,连接AD、CF,线段AD与CF之间有怎样的数量关系?试证明你的结论;
(2)操作2,如图2,将正方形ODEF沿着射线DB以每秒1个单位的速度平移,平移后的正方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;
(3)操作3:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转90°得到正方形OHKL,如图4,求△ACK的面积.

(1)操作1:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转45°得到正方形ODEF,如图2,连接AD、CF,线段AD与CF之间有怎样的数量关系?试证明你的结论;
(2)操作2,如图2,将正方形ODEF沿着射线DB以每秒1个单位的速度平移,平移后的正方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;
(3)操作3:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转90°得到正方形OHKL,如图4,求△ACK的面积.

(1)相等 见解析 (2)见解析 (3)8
解:(1)相等
由旋转的性质得∠AOB=∠COF,
在△AOD和△COF中,
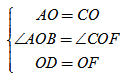
∴△AOD≌△COF(SAS),
∴AD=CF;
(2)①当0≤x≤4 ﹣4时,y=22﹣
﹣4时,y=22﹣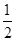 (2﹣x)2=﹣
(2﹣x)2=﹣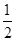 x2+2x+2;
x2+2x+2;
②当4 ﹣4≤x≤2时,y=22﹣
﹣4≤x≤2时,y=22﹣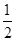 (2﹣x)2﹣
(2﹣x)2﹣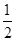 (4+x﹣4
(4+x﹣4 )2;
)2;
③2≤x≤4 ﹣2时,y=22﹣
﹣2时,y=22﹣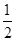 (4+x﹣4
(4+x﹣4 )2;
)2;
④4 ﹣2≤x≤4
﹣2≤x≤4 时,y=
时,y=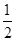 (4
(4 ﹣x)2
﹣x)2
⑤x≥4 时,y=0.
时,y=0.
(3)连接OK,

∵∠COK=∠ACO=45°,
∴OK∥AC,
∴S△ACK=S△AOC=8.
(1)根据旋转的性质得到∠AOB=∠COF,然后证得△AOD≌△COF后即可证得AD=CF;
(2)分当0≤x≤4 ﹣4时、当4
﹣4时、当4 ﹣4≤x≤2时,2≤x≤4
﹣4≤x≤2时,2≤x≤4 ﹣2时、4
﹣2时、4 ﹣2≤x≤4
﹣2≤x≤4 时、x≥4
时、x≥4 时五种情况列出两个变量之间的函数关系式即可;
时五种情况列出两个变量之间的函数关系式即可;
(3)连接OK,利用内错角相等得到OK∥AC,然后得到S△ACK=S△AOC=8.
由旋转的性质得∠AOB=∠COF,
在△AOD和△COF中,
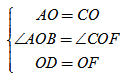
∴△AOD≌△COF(SAS),
∴AD=CF;
(2)①当0≤x≤4
 ﹣4时,y=22﹣
﹣4时,y=22﹣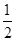 (2﹣x)2=﹣
(2﹣x)2=﹣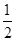 x2+2x+2;
x2+2x+2;②当4
 ﹣4≤x≤2时,y=22﹣
﹣4≤x≤2时,y=22﹣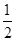 (2﹣x)2﹣
(2﹣x)2﹣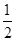 (4+x﹣4
(4+x﹣4 )2;
)2;③2≤x≤4
 ﹣2时,y=22﹣
﹣2时,y=22﹣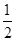 (4+x﹣4
(4+x﹣4 )2;
)2;④4
 ﹣2≤x≤4
﹣2≤x≤4 时,y=
时,y=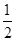 (4
(4 ﹣x)2
﹣x)2⑤x≥4
 时,y=0.
时,y=0.(3)连接OK,

∵∠COK=∠ACO=45°,
∴OK∥AC,
∴S△ACK=S△AOC=8.
(1)根据旋转的性质得到∠AOB=∠COF,然后证得△AOD≌△COF后即可证得AD=CF;
(2)分当0≤x≤4
 ﹣4时、当4
﹣4时、当4 ﹣4≤x≤2时,2≤x≤4
﹣4≤x≤2时,2≤x≤4 ﹣2时、4
﹣2时、4 ﹣2≤x≤4
﹣2≤x≤4 时、x≥4
时、x≥4 时五种情况列出两个变量之间的函数关系式即可;
时五种情况列出两个变量之间的函数关系式即可;(3)连接OK,利用内错角相等得到OK∥AC,然后得到S△ACK=S△AOC=8.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
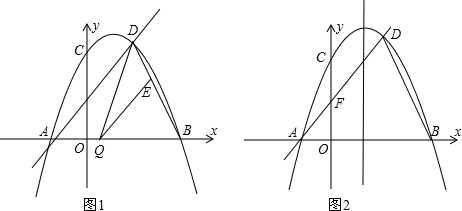
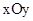 中,抛物线
中,抛物线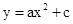 与x轴交于点A(-2,0)和点B,与y轴交于点C(0,
与x轴交于点A(-2,0)和点B,与y轴交于点C(0,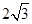 ),线段AC上有一动点P从点A出发,以每秒1个单位长度的速度向点C移动,线段AB上有另一个动点Q从点B出发,以每秒2个单位长度的速度向点A移动,两动点同时出发,设运动时间为t秒.
),线段AC上有一动点P从点A出发,以每秒1个单位长度的速度向点C移动,线段AB上有另一个动点Q从点B出发,以每秒2个单位长度的速度向点A移动,两动点同时出发,设运动时间为t秒.
 DB.
DB.

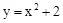 向下平移3个单位,那么所得新抛物线的表达式是 .
向下平移3个单位,那么所得新抛物线的表达式是 . ),当t =4秒时:
),当t =4秒时:
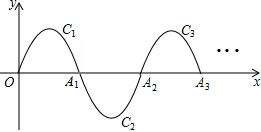
 上的概率为( )
上的概率为( ) B.
B. C.
C. D.
D.