题目内容
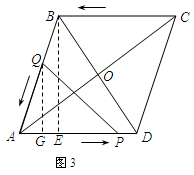
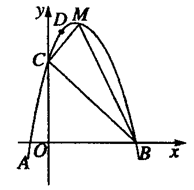
如图1,在菱形ABCD中,对角线AC、BD相交于点O,AC=8,BD=6.现有两动点P、Q分别从A、C两点同时出发,点P以每秒1个单位长的速度由点A向点D做匀速运动,点Q沿折线CB—BA向点A做匀速运动.
(1)点P将要运行路径AD的长度为 ;点Q将要运行的路径折线CB—BA的长度为 .
(2)当点Q在BA边上运动时,若点Q的速度为每秒2个单位长,设运动时间为t秒.
①求△APQ的面积S关于t的函数关系式,并求自变量t的取范围;
②求当t为何值时,S有最大值,最大值是多少?
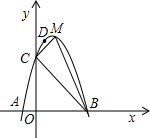
(3)如图2,若点Q的速度为每秒a个单位长(a≤ ),当t =4秒时:
),当t =4秒时:
①此时点Q是在边CB上,还是在边BA上呢?
②△APQ是等腰三角形,请求出a的值.

(1)点P将要运行路径AD的长度为 ;点Q将要运行的路径折线CB—BA的长度为 .
(2)当点Q在BA边上运动时,若点Q的速度为每秒2个单位长,设运动时间为t秒.
①求△APQ的面积S关于t的函数关系式,并求自变量t的取范围;
②求当t为何值时,S有最大值,最大值是多少?
(3)如图2,若点Q的速度为每秒a个单位长(a≤
 ),当t =4秒时:
),当t =4秒时:①此时点Q是在边CB上,还是在边BA上呢?
②△APQ是等腰三角形,请求出a的值.

(1)5;10;(2)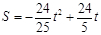 (
(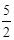 ≤t<5);
≤t<5);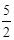 ,6;(3)CB,
,6;(3)CB,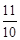 .
.
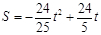 (
(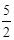 ≤t<5);
≤t<5);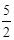 ,6;(3)CB,
,6;(3)CB,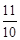 .
.试题分析:(1)根据菱形的性质可知AC⊥BD,且AC与BD互相平分,再根据勾股定理即可求出菱形的边长;
(2)①当0<t≤
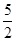 时,由题意,得AP=t,点Q在BC上运动,过点B作BE⊥AD,垂足为E,由直角三角形的性质求出BE的长,由三角形的面积公式可得到S与t的关系式;
时,由题意,得AP=t,点Q在BC上运动,过点B作BE⊥AD,垂足为E,由直角三角形的性质求出BE的长,由三角形的面积公式可得到S与t的关系式;②当
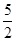 ≤t<5时,点Q在BA上运动,由题意,得AP=t,AQ=10-2t,过点Q作QG⊥AD,垂足为G,则QG∥BE,可得出△AQG∽△ABE,由相似三角形的对应边成比例即可得出S关于t的关系式,再根据二次函数的最值问题进行解答即可;
≤t<5时,点Q在BA上运动,由题意,得AP=t,AQ=10-2t,过点Q作QG⊥AD,垂足为G,则QG∥BE,可得出△AQG∽△ABE,由相似三角形的对应边成比例即可得出S关于t的关系式,再根据二次函数的最值问题进行解答即可;(3)先判断出等腰三角形的两腰长,过点Q作QM⊥AP,垂足为点M,QM交AC于点F,根据△AMF∽△AOD∽△CQF,可得出FM的值,由QF=MQ-FM得出QF的值,进而可得出a的值.
试题解析:(1)5;10
(2)当点Q在BA上运动时,5≤2t<10,即
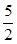 ≤t<5时.
≤t<5时.如图,过点B作BE⊥AD,垂足为E,过点Q作QG⊥AD,垂足为G,则QG∥BE.
由题意可得BE=
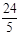 , AP= t,AQ=10-2t.
, AP= t,AQ=10-2t.∴△AQG∽△ABE, ∴
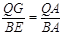 ,
,∴QG=
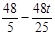 .
.∴
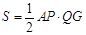 ,
,即
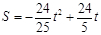 (
(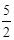 ≤t<5) .
≤t<5) .∵
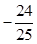 <0,所以s有最大值.
<0,所以s有最大值.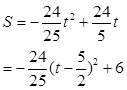
∴当t=
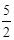 时,S的最大值为6.
时,S的最大值为6.(3) 解:∵a≤
 ,则4a≤5,
,则4a≤5,∴点Q在CB上,
作QM⊥AD于M,QM交AC于点F,则QM为菱形的高.

由前面可知,QM=
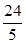 =4.8
=4.8而当点P运行到点M时,QM最小,
所以PQ≥QM,
∵t=4时,PA=4,∴QM>PA.
∴PQ≥MQ>PA,类似的AQ>MQ>PA
∴QA=QP,△APQ是等腰三角形.
∵QM⊥AP
∴AM=
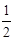 AP=2.由△AMF∽△AOD
AP=2.由△AMF∽△AOD得
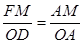 , 而AM=2,OD=3,OA=4
, 而AM=2,OD=3,OA=4∴
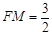 ,
,∴
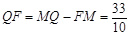 .
.由△AMF∽△CQF,
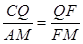 ,而QF=
,而QF=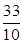 ,FM=
,FM= ,AM=2.
,AM=2.∴CQ=
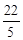 .
.而当t=4时,CQ=4a
所以4a=
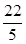 ,解得a=
,解得a=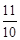 .
.
练习册系列答案
相关题目

 ,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示,其中点A为抛物线的顶点.
,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示,其中点A为抛物线的顶点.
 的图象与
的图象与 轴相交于点
轴相交于点 ,顶点为
,顶点为 ,点
,点 在这个二次函数图象的对称轴上.若四边形
在这个二次函数图象的对称轴上.若四边形 是一个边长为2且有一个内角为
是一个边长为2且有一个内角为 的菱形.求此二次函数的表达式.
的菱形.求此二次函数的表达式.
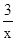 的交点的横坐标x0的取值范围是( )
的交点的横坐标x0的取值范围是( )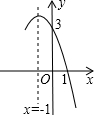
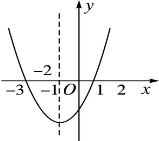
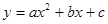 的图象如图,其对称轴x=-1,给出下列结果
的图象如图,其对称轴x=-1,给出下列结果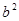 >4ac,②abc>0,③2a+b=0,④a+b+c>0,⑤a-b+c<0,则正确的结论是( )
>4ac,②abc>0,③2a+b=0,④a+b+c>0,⑤a-b+c<0,则正确的结论是( )