题目内容
如图,在等腰梯形 中,
中,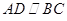 ,
, ,
, ,
,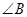 =
= .直角三角板含
.直角三角板含 角的顶点
角的顶点 在边
在边 上移动,一直角边始终经过点
上移动,一直角边始终经过点 ,斜边与
,斜边与 交于点
交于点 .若
.若 为等腰三角形,则
为等腰三角形,则 的长等于 .
的长等于 . 
 中,
中,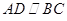 ,
, ,
, ,
,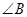 =
= .直角三角板含
.直角三角板含 角的顶点
角的顶点 在边
在边 上移动,一直角边始终经过点
上移动,一直角边始终经过点 ,斜边与
,斜边与 交于点
交于点 .若
.若 为等腰三角形,则
为等腰三角形,则 的长等于 .
的长等于 . 
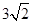 或
或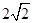 (如右图所示)
(如右图所示)
解:过D作DH⊥BC于H,
有三种情况:
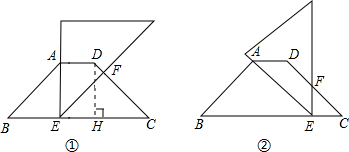
如图所示:①当AE=BE时,
∵四边形ABCD是等腰梯形,
∴BE=CH=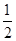 (BC-AD)=4,
(BC-AD)=4,
由勾股定理得:AB=4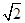 ,
,
∴CE=BC-BE=6,
∵∠B=∠BAE=45°,
∴∠AEB=90°,
∴∠FEC=180°-90°-45°=45°=∠C,
∴∠EFC=180°-45°-45°=90°,
∴由勾股定理得:CF=EF=3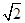 ,
,
②当AB=AE=4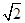 时,
时,
由勾股定理求得:BE=8,
∴CE=BC-BE=2,
同法可求出∠FEC=90°,∠EFC=45°=∠C,
由勾股定理得:CF=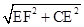 =2
=2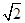 ,
,
③
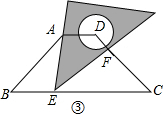
如图当AB=BE=4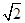 时,
时,
∠AEB=∠BAE=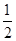 (180°-∠B)=67.5°,
(180°-∠B)=67.5°,
∴∠FEC=180°-67.5°-45°=67.5°,
∵∠C=45°,
∴∠CFE=180°-∠C-∠FEC=67.5°=∠FEC,
∴CF=CE=BC-BE=10-4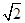 ,
,
故答案为: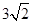 或
或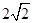 或10-4
或10-4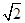
有三种情况:

如图所示:①当AE=BE时,
∵四边形ABCD是等腰梯形,
∴BE=CH=
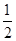 (BC-AD)=4,
(BC-AD)=4,由勾股定理得:AB=4
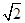 ,
,∴CE=BC-BE=6,
∵∠B=∠BAE=45°,
∴∠AEB=90°,
∴∠FEC=180°-90°-45°=45°=∠C,
∴∠EFC=180°-45°-45°=90°,
∴由勾股定理得:CF=EF=3
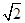 ,
,②当AB=AE=4
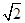 时,
时,由勾股定理求得:BE=8,
∴CE=BC-BE=2,
同法可求出∠FEC=90°,∠EFC=45°=∠C,
由勾股定理得:CF=
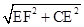 =2
=2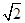 ,
,③

如图当AB=BE=4
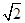 时,
时,∠AEB=∠BAE=
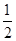 (180°-∠B)=67.5°,
(180°-∠B)=67.5°,∴∠FEC=180°-67.5°-45°=67.5°,
∵∠C=45°,
∴∠CFE=180°-∠C-∠FEC=67.5°=∠FEC,
∴CF=CE=BC-BE=10-4
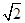 ,
,故答案为:
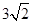 或
或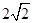 或10-4
或10-4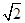

练习册系列答案
相关题目
 的边长6,点
的边长6,点 在直线
在直线 上,
上, ,连接
,连接 与对角线
与对角线 相交于点
相交于点 ,则
,则 .
.
 的红丝带交叉成60°角重叠在一起(如图),则重叠四边形的面积为_______
的红丝带交叉成60°角重叠在一起(如图),则重叠四边形的面积为_______



