题目内容
【题目】如图,两个反比例函数y1= ![]() (其中k1>0)和y2=
(其中k1>0)和y2= ![]() 在第一象限内的图象依次是C1和C2 , 点P在C1上,矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为 .
在第一象限内的图象依次是C1和C2 , 点P在C1上,矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为 . 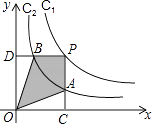
【答案】![]()
【解析】解:如图 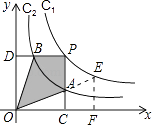 ,
,
∵B、C反比例函数y2= ![]() 的图象上,
的图象上,
∴S△ODB=S△OAC= ![]() ×3=
×3= ![]() ,
,
∵P在反比例函数y1= ![]() 的图象上,
的图象上,
∴S矩形PDOC=k1=6+ ![]() +
+ ![]() =9,
=9,
∴图象C1的函数关系式为y= ![]() ,
,
∵E点在图象C1上,
∴S△EOF= ![]() ×9=
×9= ![]() ,
,
∴ ![]() =
= ![]() =3,
=3,
∵AC⊥x轴,EF⊥x轴,
∴AC∥EF,
∴△EOF∽△AOC,
∴ ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】本题主要考查了比例系数k的几何意义的相关知识点,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能正确解答此题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目