题目内容
【题目】我们把有一组邻边相等,一组对边平行但不相等的四边形称作“准菱形”.
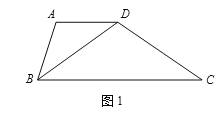
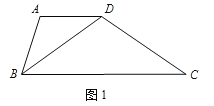
(1)证明“准菱形”性质:“准菱形”的一条对角线平分一个内角.
(要求:根据图1写出已知,求证,证明)
已知:
求证:
证明:
(2)已知.在△ABC中,∠A=90°,AB=3,AC=4.若点D,E分别在边BC,AC上,且四边形ABDE为“准菱形”.请在下列给出的△ABC中,作出满足条件的所有“准菱形”ABDE,并写出相应DE的长.(所给△ABC不一定都用,不够可添)
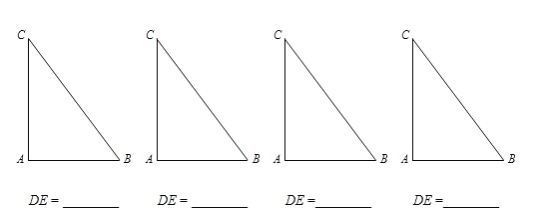
【答案】(1)答案见解析;(2)答案见解析.
【解析】
(1)根据准菱形的定义写出已知,结合图形写出求证,利用平行线的性质定理进行证明;
(2)分AE=AB,DE∥AB、BA=BD,DE∥AB、EA=ED,DE∥AB、DE=BD,DE∥AB四种情况,利用相似三角形的判定定理和性质定理计算即可.
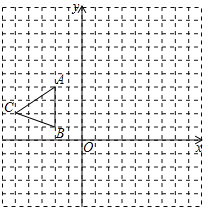
(1)已知:如图,“准菱形”ABCD中,AB=AD,AD∥BC,(![]() ).
).
求证:BD平分∠ABC.
证明:∵AB=AD,
∴∠ABD=∠BDA.
又∵AD∥BC,
∴∠DBC=∠BDA,
∴∠ABD=∠DBC.
即BD平分∠ABC.
(2)可以作出如下四种图形:
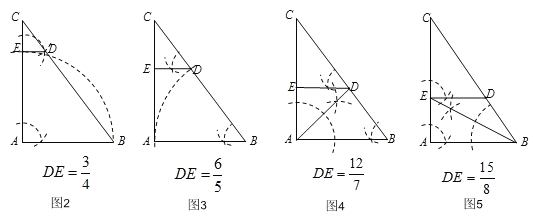
(2)可以作出如下四种图形,
∵∠A=90°,AB=3,AC=4,
∴BC=5,
如图2,当AE=AB,DE∥AB时,
![]() ,即
,即![]() ,
,
解得,DE=![]() ;
;
如图3,当BA=BD,DE∥AB时,
![]() ,即
,即![]() ,
,
解得,DE=![]() ;
;
如图4,当EA=ED,DE∥AB时,
![]() ,即
,即![]() ,
,
解得,DE=![]() ;
;
如图5,当DE=BD,DE∥AB时,
![]() ,即
,即![]() ,
,
解得,DE=![]() .
.
故答案为:![]() ,
,![]() ,
,![]() ,
,![]() .
.

练习册系列答案
相关题目